Apostilas sobre a entropia.
Quando criou o mundo, o Todo Poderoso introduziu apenas a Primeira Lei da Termodinâmica e a Conservação da Energia. O maná surgia do nada, ninguém envelhecia e as alegrias do passado podiam ser revisitadas a qualquer momento. Era um paraíso! Mas, Adão e Eva acharam de cometer o pecado original e o Criador castigou-os (e a nós, que não tivemos nada com isso!), inventando a Segunda Lei da Termodinâmica e a Entropia. E até hoje a gente tem de ganhar o pão com o suor do rosto.
Isso é só um chiste, é claro, mas é verdade que a gente tem de suar por causa da entropia. E o que é mesmo a entropia? Todo mundo sabe, com mais ou menos precisão, o que é a energia. E sabe que a energia se apresenta de várias formas, mecânica, calorífica, química, nuclear etc. Todas, porém, são manifestações de uma mesma grandeza física. E sabe que o valor total da energia se conserva, enquanto ela se transforma de um tipo para o outro.
Já a entropia é a prima pobre, pouco falada (e mal-falada, por sinal) e ainda menos compreendida. E, no entanto, ela é tão importante e afeta tanto nossa vida diária quanto a energia. Nas páginas seguintes, vou tentar dar uma ideia do significado da entropia. Veremos que, diferentemente da energia, ela não se conserva. Essa, aliás, é uma das razões de seu mistério e seu charme um tanto fatalístico. Enquanto a energia é uma fada que tudo permite (até transformar jerimum em carruagem), a entropia parece mais uma bruxa malvada e desmancha-prazeres que impõe condições e regras de funcionamento. Começaremos falando da ciência da termodinâmica, de onde surgiu, inicialmente, a ideia de entropia.
Apostila 1: A primeira lei da termodinâmica.
O significado técnico do termo energia não difere muito do que usamos na vida diária. Para nosso propósito nesse relato, basta não confundir energia com força e saber que a energia se conserva. Algumas formas mais comuns da energia são: a energia cinética, ou energia de movimento; a energia elétrica, que move nossos eletrodomésticos e cujo preço pagamos todo mês; a energia química, presente em uma bateria de carro e em nossos corpos; a energia nuclear, que reside no interior dos átomos e se manifesta nos reatores e nas bombas. Todas essas formas podem ser tratadas como equivalentes, com a mesma unidade de medida, e podem se transformar umas nas outras, quando as condições são favoráveis.
A energia tem várias unidades, usadas conforme a conveniência. Por exemplo, a energia calorífica é medida em calorias, a energia de movimento é medida em joules e a energia elétrica que consumimos é medida em quilowatts-hora. Mas, como toda forma de energia termina sendo uma manifestação diferente da mesma coisa, é sempre possível passar de uma unidade para outra por uma relação simples. Por exemplo, 1 caloria é igual a 4,18 joules, e podemos falar, por exemplo, de quantos joules tem um dado alimento.

O resultado mais importante acerca da energia é que ela se conserva. A energia elétrica que entra em sua casa é registrada no medidor em quilowatts-hora (kw-h). Essa energia é toda transformada em outros tipos de energia mas, no cômputo geral, a quantidade que entra é usada ou desperdiçada, mas não desaparece. Os joules, ou kw-h, que você paga no fim do mês são transformados em energia luminosa (nas lâmpadas), em energia cinética (no liquidificador), em calor etc, mas as quantidades de energia fornecida e transformada são iguais.
Conta de luz típica. Veja o preço do quilowatt-hora em 1999.
Ao fazer medidas de energia, os físicos consideram uma determinada região e observam todas as variações de energia nessa região. Por exemplo, essa dita região pode ser sua casa. Vamos usar o termo técnico e dizer que sua casa é o sistema. Tudo que está fora de sua casa são os arredores. O conjunto de sua casa e o que está fora (sistema+arredores), será chamado, tecnicamente, de universo, com u minúsculo, para distinguir do outro (maiorzinho) que tem o mesmo nome. Pois bem, toda energia trocada entre o sistema e seus arredores deve se conservar. Isto é, qualquer quantidade de energia que passa de uma parte para a outra, deve ser usada, transformada ou devolvida, sem ganhos nem perdas.
Essa é a essência da chamada Primeira Lei da Termodinâmica. Ela pode ser formulada, de forma simples, nos seguintes termos:
“Em todo processo natural, a energia do universo se conserva.”
Usei o termo “universo”, com u minúsculo, pois o exemplo envolvia apenas sua casa e seus arredores. Mas, nada impede de usar o termo Universo e generalizar a Lei de forma mais ampla. No caso do Universo cosmológico, fica difícil saber o que seriam os arredores, pois qualquer coisa que exista sempre faz parte do Universo. Nesse caso, o sistema é fechado, não tem arredores para trocar energia. Mas, assim mesmo, a energia se conserva. Isto é, podemos supor que a energia total existente no Universo se conserva, nunca aumentando nem diminuindo.
É impossível construir uma máquina que gere energia do nada. Uma máquina que fizesse tal coisa seria um “moto perpétuo da primeira espécie”, e não existe porque contradiz a Primeira Lei da Termodinâmica. Quando você ouvir falar de motores que funcionam sem combustível, tirando energia do nada, pode ficar seguro que é fraude.
Apostila 2: A segunda lei da termodinâmica.
Para apresentar a Segunda lei da Termodinâmica vou descrever alguns experimentos simples e salientar o que eles têm em comum.
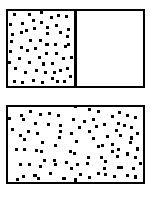
1) Nessa caixa, de um lado há um gás e do outro há o vácuo. Se retirarmos a separação veremos o gás se espalhar e ocupar todo o volume da caixa. Aí você fica, com a partição na mão, esperando que o gás volte a se concentrar só de um lado. Quando isso acontecer, você reporá a partição, restabelecendo a situação original. Espere sentado, lendo um bom livro de Física.
2) Temos duas canecas de alumínio, uma com 1 litro de água a 80oC e outra, com 1 litro de 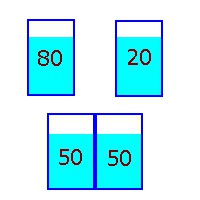 água a 20oC. Encostando uma na outra, a água quente esfria e a água fria esquenta até que ambas ficam na temperatura média de 50oC. Agora você fica esperando para ver se o inverso ocorre, passando calor, espontaneamente, de uma caneca para a outra, restabelecendo a situação original. Continue sentado, lendo seu livro.
água a 20oC. Encostando uma na outra, a água quente esfria e a água fria esquenta até que ambas ficam na temperatura média de 50oC. Agora você fica esperando para ver se o inverso ocorre, passando calor, espontaneamente, de uma caneca para a outra, restabelecendo a situação original. Continue sentado, lendo seu livro.
Eu poderia citar inúmeros processos como esses: copos que se quebram ao cair no chão, pilhas de lanterna que se descarregam, gelo que se derrete dentro do guaraná e assim vai. O que todos esses processos têm em comum é que podem ocorrer em um sentido mas não ocorrem, espontaneamente, no sentido oposto. São processos de mão única. Em termos mais técnicos, eles são chamados de processos irreversíveis, pois não revertem espontaneamente.
No entanto, esses processos poderiam se dar em qualquer dos dois sentidos sem contrariar a Primeira Lei da Termodinâmica. Isto é, sem violar o princípio da conservação da energia. Veja, por exemplo, o caso dos canecos com água. Uma certa quantidade de calorias (energia térmica) passa da água quente para a fria até que as duas canecas ficam com a mesma temperatura. Se começarmos com as duas canecas com água a 50oC e, por algum acaso, a mesma quantidade de calorias passar de um caneco para o outro, um caneco ficará a 80oC e o outro a 20oC. Como o calor perdido por um foi ganho pelo outro, teria havido conservação de energia. Mas, a gente sabe que esse processo inverso nunca ocorre.
A Segunda Lei da Termodinâmica expressa essa mania da natureza de estabelecer um sentido para os processos naturais espontâneos. Existem vários modos de enunciar essa Lei. Uma delas, devida a Rudolph Clausius, diz assim:
“É impossível haver transferência espontânea de calor de um objeto frio para outro mais quente.”
Observe a condição “espontanea”. Em sua geladeira, a todo instante passa calor de dentro para fora, resfriando o interior e aquecendo o exterior. Mas, isso só acontece se a geladeira estiver ligada na tomada e funcionando, isto é, consumindo energia elétrica. O processo, portanto, não é espontâneo, tem de ser induzido.

Veja esse maravilhoso projeto de um um engenhoso engenheiro para uma hipotética fábrica de gelo. Para não ter de pagar a conta da luz no fim do mês, nosso engenheiro pretende aproveitar o calor que sai da geladeira para produzir vapor; esse vapor é usado para mover uma turbina; a turbina aciona um gerador elétrico que, finalmente, produz a corrente elétrica necessária para manter a geladeira funcionando. Calculando cuidadosamente todas as trocas de energia nas várias partes do projeto ele observa que há um balanço perfeito. A energia é conservada e o gelo foi produzido de graça!
No entanto, esse projeto está furado. Simplificando o desenho podemos observar que todo esse processo se resume em retirar calor de um tanque e passar esse calor para o resto da engenhoca sem apelar para nenhum recurso externo. Isso contraria a Segunda Lei da Termodinâmica e, portanto, não funciona. É o que se chama de “moto perpétuo de segunda espécie”, dispositivo ardentemente buscado por malucos de vários tipos, mas proibido pelas leis da natureza.
O projeto da parte de cima equivale a congelar a água de um tanque sem receber energia externa.
Como saber se um processo viola, ou não, a Segunda Lei da Termodinâmica? Isto é, como decidir se esse processo está na mão certa e é um processo natural, ou não? Bem, é aí que surge o conceito de ENTROPIA, que veremos a seguir.
Apostila 3: Apresentando a entropia.
Vimos que, em qualquer processo natural a ENERGIA TOTAL do universo (isto é, do objeto considerado e tudo mais que interage com ele) se conserva (fica constante). No entanto, alguns processos que conservam energia não ocorrem naturalmente. Para saber que tipo de processo pode ou não ocorrer naturalmente os físicos inventaram uma grandeza chamada ENTROPIA. Essa grandeza física pode, em tese, ser medida para qualquer objeto por alguma técnica que não nos interessa descrever por enquanto. Mas, mesmo sem saber ainda o que é a entropia, basta saber o seguinte: em um processo natural a entropia do universo (isto é, a soma da entropia do objeto com a entropia de seus arredores) SEMPRE AUMENTA. Aliás, pode-se considerar isso como outra forma de enunciar a Segunda Lei da Termodinâmica:
“Em qualquer processo natural a ENTROPIA do universo sempre aumenta.”
Portanto, a receita para saber se um processo pode ocorrer naturalmente (espontaneamente), ou não, é a seguinte:
1) Mede-se, de algum modo, a Entropia Total do objeto e de seus arredores (isto é, a entropia do “universo”).
2) Deixa-se o processo ocorrer (pelo menos, mentalmente) e observa-se o que acontece com a Entropia Total durante o processo.
3) Se a Entropia Total aumentar, o processo é natural, permitido pela Segunda Lei da Termodinâmica e pode ocorrer espontaneamente. Se a Entropia Total quiser diminuir, o processo

Veja, de novo, o caso das duas canecas com água. Se a gente conseguir medir a entropia desse sistema vai constatar que a entropia das canecas separadas, com temperaturas desiguais, é menor que a entropia delas quando juntas, com a mesma temperatura. Logo, um processo natural pode ocorrer no sentido de igualar as temperaturas mas nunca no sentido inverso.
Resta saber como MEDIR a entropia de um sistema, do universo ou até do Universo. Os fundadores da Termodinâmica, entre eles Clausius, Boltzmann e Maxwell, inventaram vários métodos mais ou menos engenhosos para fazer essa medida. A seguir, descreverei, de um modo bem simplificado, um esquema bolado pelo grande físico austríaco Ludwig Boltzmann, no século 19. Para isso, usarei uma analogia com um jogo de baralho. Essa, é claro, não foi a forma descrita por Boltzmann mas servirá para nossos propósitos.
Apostila 4: A entropia no jogo de bridge.
Quando eu era uma garotinha em Sobral, tia Luzia, uma das grandes damas de minha família, ao tomar conhecimento que eu não sabia jogar bridge, decretou: “A educação dessa menina está incompleta”. Tive de aprender esse jogo que era praticado por damas e cavalheiros do império britânico. Pois agora vou fazer valer o esforço usando o jogo de bridge para explicar como se pode medir a entropia.
Não se assuste: não é preciso saber jogar bridge para entender o argumento. Nesse jogo, um baralho normal de 52 cartas é dividido, ao acaso, entre 4 jogadores, cada um recebendo uma “mão” de 13 cartas. Há um esquema de contar pontos para as cartas que é o seguinte: um Ás vale 4 pontos, um Rei vale 3 pontos, uma Dama vale 2 pontos e um Valete vale 1 ponto. As demais cartas valem zero pontos.

Digamos que José recebeu a mão de cima (sortudo!), que vale 37 pontos, e João recebeu a mão de baixo (coitado!), que vale zero pontos. Alguém pode pensar que a mão de José é muito menos provável que a de João, mas não é. Um jogador de bridge pode não concordar, mas, ambas são igualmente prováveis! Como cada carta só ocorre uma vez no baralho, tirar um rei de copas é tão difícil quanto tirar um dois de paus. Portanto, pegando,
ao acaso, 13 cartas de um baralho, é tão difícil conseguir uma mão como
a de cima quanto uma mão exatamente como a de baixo.

Há algo, porém, que distingue as duas mãos: o número de pontos. A questão certa não é saber a probabilidade de cada mão. Ambas são igualmente prováveis. A questão é saber qual é a probabilidade de receber uma mão com 37 pontos ou de receber uma mão de zero pontos. Agora, a coisa é diferente. Só existem 4 mãos diferentes que valem 37 pontos.
Todas elas são como a mão da figura de cima, apenas trocando o naipe do valete. Já uma mão de zero pontos é qualquer mão sem nenhum ás ou carta de figura. O número de mãos possíveis com zero pontos é da ordem de 2,3 bilhões!
(Para quem conhece análise combinatória: para fazer uma mão de zero pontos basta tirar os 4 ases e as 12 figuras de um baralho (16 cartas) e separar uma mão de 13 cartas a partir das 36 cartas restantes. O número de mãos distintas será a combinação de 36 cartas, tomadas 13 a 13:
C3613 = 36! / ((36-13)! 13!) = 2.310.789.600 )
Para facilitar nossa conversa, vamos usar os termos microestado e macroestado, como Boltzmann fazia. Qualquer uma dessas 2,3 bilhões de mãos será um microestado do macroestado correspondente a zero pontos. Isto é, o macroestado zero pontos tem 2,3 bilhões de microestados, enquanto o macroestado 37 pontos tem apenas 4 microestados. Agora, é fácil entender porque uma mão de zero pontos é mais provável que uma mão de muitos pontos: ela tem muito mais microestados.
Podemos, agora, definir a ENTROPIA de uma pontuação no bridge como sendo o número de mãos diferentes com essa pontuação. Ou, equivalentemente, essa entropia será o número de microestados em um macroestado. A entropia da mão de zero pontos (macroestado) é cerca de 2,3 bilhões (número de microestados), enquanto a entropia da mão de 37 pontos é apenas 4.
Como exercício, você pode calcular a entropia de uma mão de 12 pontos.
Como veremos a seguir, essa definição de entropia serve, com alguma modificação, para ser usada em qualquer sistema físico, seja uma mão de baralho, um motor de carro, um balde com água, uma estrela ou até mesmo o Universo, com U maiúsculo. Antes, vamos resumir o que vimos até aqui.
1) Um macroestado de um sistema é composto de um certo número de microestados.
2) Todos os microestados de qualquer macroestado são igualmente prováveis.
3) Quanto mais microestados um macroestado tiver, mais provável ele é.
4) A entropia de um macroestado é proporcional ao número de microestados que ele tem.
Apostila 5: Entropia, probabilidade e desordem.
A definição de “ENTROPIA” que apresentei na seção anterior precisa ser modificada para corresponder melhor com a definição técnica, usada pelos físicos. Como vimos, a entropia de um macroestado é proporcional ao número de microestados nesse macroestado. E sabemos que a probabilidade de um macroestado ocorrer proporcional ao número de microestados que ele contém. Basta lembrar o exemplo das mãos de bridge para entender isso. No entanto, há um problema. A entropia pode ser definida de outras maneiras e nessas maneiras ela é uma quantidade aditiva. Isso significa o seguinte. Se um sistema A tem entropia SA e um sistema B tem entropia SB, um sistema C, composto dos sistemas A e B, deve ter entropia SC = SA + SB.
No entanto, probabilidades são quantidades multiplicativas. Por exemplo, a probabilidade de obtermos um CINCO, ao lançarmos um dado, é 1/6. Se lançarmos dois dados, a probabilidade de obtermos dois CINCOS consecutivos é 1/6 x 1/6 = 1/36.
Entropias se somam, mas, probabilidades se multiplicam. Como, então, relacionar a entropia de um estado com a probabilidade desse estado? Para contornar essa dificuldade, Boltzmann optou por definir a Entropia como proporcional ao logaritmo da probabilidade do macroestado.
Lembre da matemática que aprendeu no colégio: se tivermos C = A x B, teremos log C = log A + log B.
Portanto, se um sistema tem um macroestado A, com probabilidade WA e entropia SA, e outro sistema tem um macroestado B, com probabilidade WB e entropia SB, a probabilidade de achar o conjunto dos dois sistemas nesses estados, simultaneamente, será W = WA x WB, que corresponde à entropia total S.
Tomando os logaritmos nos dois lados, temos log W = log WA + log WB.
Então, se dissermos que a entropia do macroestado A é SA = k x log WA, e a entropia do macroestado B é SB = k x log WB, teremos
S = SA + SB, onde S = k x log W é a entropia dos estados A e B juntos.
Desse modo, segundo Ludwig Boltzmann, a entropia S de um sistema que está em um estado cuja probabilidade é W, é escrita como S = k x log W. Essa constante de proporcionalidade k é chamada de constante de Boltzmann. Outra vantagem de usar essa definição da entropia ligada ao logaritmo da probabilidade decorre do fato de que, em geral, estaremos lidando com números muito grandes. Melhor que manusear um número como 100.000.000.000, por exemplo, é usar seu logaritmo que vale 11 (igual ao número de zeros), bem mais doméstico. Nos casos reais da física, o número de microestados costuma ser gigantesco.
O logaritmo usado na fórmula de Boltzmann é o logaritmo natural (base e), e não o decimal (base 10), mas, o argumento é o mesmo.

Considere, por exemplo, o problema de contar os microestados possíveis em uma caixa com um gás como o ar. Para isso, podemos imaginar a caixa dividida em seções e contar quantas moléculas tem cada seção. Um macroestado A, como na figura de cima, seria aquele em que a seção 1 tem 3 moléculas, a seção 2 tem 4, e assim por diante. A probabilidade desse macroestado seria dada pelo número de maneiras distintas (microestados) de distribuir as moléculas mantendo a configuração. Por exemplo, trocando uma molécula da seção 1 com outra da seção 2, teríamos um microestado diferente, correspondente ao mesmo macroestado.
Duas coisas são claras. Primeiro, se o número de moléculas for grande, o número de microestados correspondentes a um dado macroestado é enorme. Segundo, é fácil ver que um macroestado como o de cima é muito mais provável que um macroestado como o de baixo, pois o de cima tem muito mais microestados.
Se o gás fosse colocado na caixa do jeito mostrado na figura de baixo, em um instantinho ele se espalharia e teria um jeitão parecido com a figura de cima. Agora, veja: a probabilidade de se encontrar o gás nos dois jeitos é exatamente a mesma! Lembre do caso das mãos de bridge. Entretanto, o número de jeitos (microestados) de distribuir as moléculas de modo a ter o mesmo número em cada seção (macroestado) é diferente, nos dois casos. Esse número é muito maior para a configuração da figura de cima. Isto é, a entropia do gás na figura de cima é muito maior que a entropia na figura de baixo. Isso nos leva a outra maneira (mais uma!) de enunciar a Segunda Lei da Termodinâmica:
“Todo sistema físico sempre evolui, espontaneamente, para situações de máxima entropia.”
O número de microestados pode, também, ser usado como uma medida da desordem do sistema. Nesse contexto, a desordem do gás na figura de cima é maior que a desordem na figura de baixo. E isso nos leva a mais uma forma de enunciar a Segunda Lei da Termodinâmica:
“Todo sistema natural, quando deixado livre, evolui para um estado de máxima desordem, correspondente a uma entropia máxima.”
Agora, pense em alguns eventos naturais, desses que ocorrem a todo instante. Um copo que cai e se quebra, um papel que se queima, uma xícara de café que esfria, uma pilha que descarrega, a gente que envelhece, “a vida inteira que poderia ter sido e que não foi”. Nada disso precisaria acontecer, ou, se acontesse, poderia sempre ser revertido, se não existisse a danada da Segunda Lei da Termodinâmica.
Apostila 6: As atribulações de Ludwig Boltzmann.
No túmulo de Ludwig Boltzmann, no Cemitério Central de Viena, pode-se ver a imagem do criador da Física Estatística e, acima dela, a famosa equação:

Túmulo de Bolzmann em Viena Fotografado por Constantino Tsallis
S = k log W.
O curioso é que Boltzmann nunca escreveu essa equação. Ela apareceu, pela primeira vez, no livro Teoria do Calor, de Max Planck, publicado em 1906, ano da morte de Boltzmann. Até a constante k, hoje chamada de constante de Boltzmann, foi introduzida na literatura por Planck.
Mas, isso não tem nenhuma importância, pois Boltzmann foi o primeiro e o mais ativo defensor da idéia de explicar os fenômenos macroscópicos (pressão, temperatura etc) através de interações entre átomos e moléculas em constante movimento.
Hoje, qualquer criança de jardim da infância sabe o que é um átomo e aceita, com naturalidade, sua existência. No final do século 19, porém, muitos físicos e químicos de renome não aceitavam a idéia de que a matéria é descontínua. As opinões de Boltzmann foram contestadas com veemência por Ernest Mach e Wilhelm Ostwald e as desavenças, em certos momentos, saíram da arena puramente científica, entrando na disputa pessoal.
No entanto, Boltzmann não estava só, nessa disputa. Alguns dos maiores sábios da Europa e dos Estados Unidos sempre o apoiaram. Inúmeras honrarias e títulos lhe foram concedidos pelas mais conceituadas universidades. O próprio Max Planck, um de seus maiores fãs, escreveu, em 1904:
“Clausius e Maxwell nunca tentaram dar uma definição direta da entropia em termos mecânicos. Esse passo foi dado por Boltzmann, a partir da teoria cinética dos gases, definindo a entropia de forma geral e inequívoca, como o logaritmo da probabilidade de um estado mecânico.”
Mas, Ludwig Boltzmann era um cara depressivo. Por causa das desavenças com alguns colegas, como os que citamos acima, ele mudava constantemente de universidade, tendo passado, em poucos anos, por Viena, Graz, Leipzig, Heidelberg e Berlim. Em 1900, quando estava em Leipzig, tentou o suicídio, talvez por causa de suas controvérsias com Ostwald. Em 1902, voltou para Viena mas sua saúde, física e mental, definhava. Em 1906, quando passava férias na Baía de Druino, perto de Trieste, Boltzmann se enforcou. Não se sabe ao certo se as acirradas disputas científicas que ainda o acompanhavam pesaram para que ele encarasse esse trágico fim.
Pouco tempo depois de sua morte as evidências experimentais da validade de suas idéias começaram a se acumular rapidamente. Medidas de J. Perrin, em 1908, mostraram de forma inequívoca a existência e o movimento dos átomos e moléculas e sua concordância perfeita com as previsões teóricas de Boltzmann.
(NOTA DO EDITOR: Veja O MOVIMENTO BROWNIANO.)
Juntamente com o americano Josiah Gibbs, que trabalhou na mesma linha que ele, de forma independente, Boltzmann é considerado o criador da Mecânica Estatística, um dos ramos mais importantes e frutíferos da Física Moderna.
Apostila 7: Entropia de um buraco negro.
Quando os estudos sobre buracos negros começaram a esquentar, aí pela década de 70 do século passado, surgiu uma complicação. Um buraco negro, como se sabe, engole tudo que chega perto dele. Toda matéria que penetra em um buraco negro está perdida para o resto do Universo. Como nem a própria luz pode escapar de um buraco negro, nada podemos saber do que se passa dentro dele, a não ser por suposições teóricas.
Uma das características de um buraco negro dos grandes é um jato de gás relativístico que se estende por milhares de anos-luz. Na imagem à direita vemos a Galáxia PG 0052+251, fotografada pelo Telescópio Espacial Hubble, que pode ter um gigantesco buraco negro em seu núcleo.


O paradoxo era o seguinte: ao engulir matéria, o buraco negro engole a entropia dessa matéria. E, nada parece acontecer do lado de fora para compensar essa perda de entropia do Universo. Portanto, a Segunda Lei da Termodinâmica estaria sendo violada nas proximidades de um buraco negro (bem feito!).
Alguns físicos não ficaram satisfeitos com esse resultado. Violar uma lei fundamental como essa não é assim tão simples. Jacob Bekenstein, físico israelense, propôs que os buracos negros deveriam, também eles, ter entropia, que deveria crescer com a matéria engolida. Bekenstein calculou de quanto a entropia de um buraco negro aumentaria com a massa engolida e achou números enormes. Acreditar nesses números implicava em acreditar que os átomos e moléculas engolidos pelo buraco negro estariam em um tremendo grau de desordem. Ninguém ainda sabe direito o que se passa dentro de um buraco negro, já que nada pode sair de lá para contar alguma história. Mas, uma coisa é certa: se o buraco negro tem entropia, ele também tem uma temperatura. E, se tem temperatura, deve emitir radiação.
Os estudos de Bekenstein foram encarados com ceticismo pela comunidade de astrofísicos até que o russo Yakov Zel’dovich e o inglês Stephen Hawking, usando as armas da mecânica quântica associadas à relatividade geral de Einstein, mostraram que os buracos negros realmente emitem radiação. Hawking calculou que a entropia de um buraco negro é proporcional à área de sua superfície que, por sua vez, é inversamente proporcional ao quadrado de sua massa.
Esse surpreendente resultado serviu para aumentar ainda mais o prestígio da Segunda Lei da Termodinâmica. Mesmo em situações extremas, como nas beiradas de um buraco negro, a entropia sempre aumenta. Não há perdão.

