Problemas Famosos da Matemática
Há quem diga que a Matemática é mais que um código de símbolos obedecendo uma lógica própria. Para esses extremistas, a própria natureza já tem uma estrutura matemática e a tarefa dos físicos é desvendá-la.
O grande físico inglês Paul Dirac colocava a beleza matemática um nível acima da observação dos fenômenos naturais. Segundo ele, “é cada vez mais evidente que as regras que o matemático acha interessantes são as mesmas que a natureza escolheu”. Por esse ponto de vista, o trabalho do físico teórico não consiste em formalizar as descobertas dos experimentais, mas, de preferência, procurar belas equações que se ajustem às peculiaridades da natureza. Em outras palavras, as equações já estão lá, resta apenas descobrí-las.
Nessa Seção Especial, vamos relatar algumas curiosidades, com ênfase em alguns problemas clássicos da Matemática, vários deles ainda não solucionados.
A conjectura de Golbach.
Em 7 de Junho de 1742, em uma carta a Leonhard Euler, Christian Goldbach levantou a hipótese de que todo número inteiro maior que 5 pode ser escrito como a soma de três números primos. Euler gostou desse palpite e, achando pouco, modificou-o ao que passou a ser conhecido como a conjectura de Golbach:
“Todo inteiro positivo par maior ou igual a 4 pode ser escrito como a soma de dois números primos.”
Um número primo, como toda criança sabe, é um número inteiro positivo que só é divisível por 1 e por si mesmo. Exemplos de primos são: 2, 3, 5, 7, 11, 13. Existem infinitos números primos, como foi demonstrado de forma muito elegante por Euclides de Alexandria, 300 anos antes da era cristã.
A tabela ao lado mostra alguns exemplos de números pares escritos como a soma de dois números primos.Até hoje, na verdade, ninguém conseguiu demonstrar a conjectura de Goldbach. Já houve até um prêmio em dinheiro para quem conseguisse fazê-lo, mas como ninguém apareceu com uma solução, o prêmio foi retirado.
Em 1939, um matemático alemão demonstrou que todo número par pode ser escrito como a soma de, no máximo, 30.000 números primos. Chega a ser engraçado, além de estar ainda muito longe dos dois primos exigidos pela conjectura original. Recentemente, um grupo de pesquisadores usou supercomputadores e conseguiu mostrar que a conjectura está correta para inteiros até 1014!
Como vemos, proposições bastante simples podem ser extremamente complicadas de serem demonstradas. Essa conjectura, aparentemente fácil de ser demonstrada, já derrubou muita gente famosa.
Curioso, também, é o fato da conjectura já ser conhecida por muitos matemáticos mesmo antes de ser enviada na carta de Goldbach. Descartes, por exemplo, já tinha conhecimento dela. Por que então ficou com o nome de Goldbach? Como disse o matemático Erdös, “É ótimo que a conjectura tenha o nome de Goldbach, pois, matematicamente falando, Descartes é infinitamente mais rico que Goldbach”.
O tijolo de Euler.
O tijolo de Euler é um paralelepípedo regular de lados que são números inteiros A, B e C (sendo A>B>C) cujas diagonais de face, DAB, DAC e DBC, também são números inteiros. Se a diagonal principal (que liga os pontos M e N na figura) também é um número inteiro, o tijolo é dito “perfeito”. Não se conhece nenhum exemplo de um tijolo de Euler perfeito.
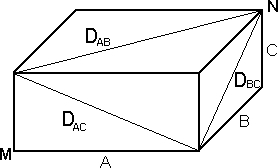
O tijolo de Euler simples, imperfeito, com os menores valores para A, B e C que se conhece tem A = 240, B = 117 e C = 44. As diagonais são: DAB = 267, DAC = 244 e DBC = 125. Foi descoberto em 1719, pelo matemático Halcke.
Com o advento dos computadores ficou muito mais fácil achar tijolos de Euler. Ao que parece, já são conhecidos os 5000 menores tijolos, medidos pelo maior lado. Os 5 primeiros são:
240, 117,44
275, 252, 240
693, 480, 140
720, 132, 85
792, 231, 160
O problema matemático relacionado é achar uma ou mais fórmulas que produzam automaticamente todos os tijolos de Euler que existem. Até hoje ninguém conseguiu essas fórmulas.
Os números perfeitos.
Um número é chamado de perfeito se for igual à soma de todos seus divisores, sem repetir nenhum deles.
Por exemplo, 28 é um número perfeito pois:
28 = 1 + 2 + 4 + 7 + 14
Números desse tipo são um prato cheio para os místicos e os charlatães. Desde os velhos tempos de Pitágoras que alguns matemáticos mais espertos (ou espertalhões) ganham dinheiro dos trouxas com coisas desse tipo.
Os quatro primeiros números perfeitos são 6, 28, 496 e 8128. Foram listados por Nicômaco de Gerasa, que viveu na Palestina aí por volta do ano 100. Como se vê, não há nenhuma ordem evidente na seqüência dos números perfeitos. Será que existe alguma fórmula que aponte para todos os números perfeitos? Ninguém sabe até hoje. A teoria de números é cheia de casos como esse, de números aparentemente simples e fáceis de definir mas extremamente difíceis de sistematizar.
O maior número perfeito que se conhece, hoje em dia, parece que é:
2.305.843.008.139.952.128
Se você está desocupado e não tem nada melhor para fazer, pode muito bem verificar que esse número é mesmo a soma de todos seus divisores, sem repetição.
Uma curiosidade: em 1891, um matemático alemão (só podia ser) demonstrou que todos os números perfeitos pares terminam com 16, ou 28, ou 36, ou 56, ou 76, ou 96.
O mapa de quatro cores.
Francis Guthrie era um estudante inglês de direito, em 1852, quando perguntou a seu irmão Frederick, que estudava matemática, quantas cores eram necessárias, no máximo, para colorir um mapa sem que países com fronteiras comuns tivessem a mesma cor. Ele próprio, Francis, tinha feito alguns testes e achava que o número máximo de cores seria apenas quatro.
Frederick levou essa questão a seu professor, o conhecido matemático Augustus De Morgan que, não conseguindo resolvê-la, escreveu para outro matemático, ainda mais famoso, Lorde William Hamilton, inventor do hoje omnipresente hamiltoniano. O lorde também não conseguiu nenhum progresso e, a partir daí, o problema do estudante de direito passou a ser um dos mais famosos da história da matemática. Francis Guthrie trabalhou uns tempos como advogado mas sempre se manteve interessado em matemática, tendo até publicado vários artigos interessantes.
A “conjectura de Guthrie”, segundo a qual bastam, no máximo, quatro cores para colorir qualquer mapa sem que países (ou estados) com fronteiras comuns tenham a mesma cor, já foi testada e aprovada em um número enorme de vezes.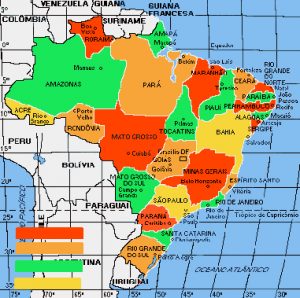
A figura ao lado mostra como conseguimos colorir um mapa do Brasil com as quatro cores mostradas nas faixas do lado esquerdo inferior. Como se pode ver, quaisquer dois estados com fronteira comum têm sempre cores diferentes, como exigido pela conjectura de Guthrie. Será possível conseguir o mesmo resultado usando apenas três cores? Talvez você queira experimentar. Podemos adiantar, porém, que não vai conseguir.
Veja que o Distrito Federal ficou com a cor de Goiás, mas, se você quiser, pode pintá-lo de verde ou vermelho, dependendo de sua preferência política.
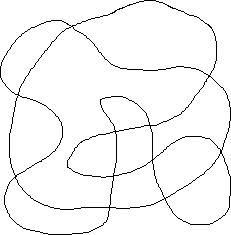
Note que, mesmo se quatro cores são necessárias – e suficientes – para colorir qualquer mapa, alguns mapas podem ser coloridos com três ou até duas cores. Tente colorir o mapa da esquerda na figura abaixo com apenas duas cores. Você não conseguirá. Mas, conseguirá fazê-lo com o mapa da direita. Na verdade, é fácil desenhar um mapa complicado que pode ser colorido só com duas cores. Basta traçar uma curva fechada sem levantar a ponta do lápis até retornar ao ponto inicial. O mapa da direita foi desenhado assim. Agora, uma perguntinha: se a gente desenhar outra curva fechada, sem levantar o lápis, por cima dessa da figura da direita, o mapa obtido poderia ser colorido só com duas cores?
Um grande número de matemáticos da pesada tentou provar a conjectura de Guthrie, sem sucesso. Herman Minkowski, que foi professor de Einstein, quando tomou conhecimento do problema disse que iria resolvê-lo em poucos dias. Depois de anos de tentativas desistiu e disse: “fui punido por minha arrogância”.
Em 1879, Alfred Kempe, outro advogado que sabia matemática, publicou uma prova do teorema na revista Nature, usando um método que ele próprio inventou, o chamado “método das correntes”. Sua prova foi comemorada com tanto entusiasmo que ele acabou sendo eleito para a Sociedade Real e feito lorde. Infelizmente, no entanto, alguns anos depois, foi mostrado que sua demonstração estava errada. Kempe concordou com a crítica e teve de admitir que não sabia corrigir os erros de sua prova.
Mesmo assim, seu trabalho não foi em vão, pois, finalmente, em 1976, 124 anos após ser enunciada, a conjectura de Guthrie acabou sendo demonstrada com o uso, entre outras técnicas, do método das correntes. Os autores da proeza foram Kenneth Appel e Wolfgang Haken, da Universidade de Illinois.
Só que a demonstração dos dois usava intensamente os computadores. O programa que escreveram tinha milhares de linhas de código e levou mais de 1200 horas para rodar. Os matemáticos mais puristas torcem o nariz para esse tipo de demonstração, preferindo os processos tradicionais da lógica matemática. Mas, até hoje, ninguém conseguiu achar algum furo no trabalho de Appel e Haken.
A conjectura de Kepler.
Qual é a forma mais compacta de empilhar esferas de mesmo raio? Esse é um problema que sempre interessou os produtores de laranjas ou maçãs que querem, com razão, economizar engradados.
Em 1611, Johannes Kepler, aquele mesmo que enunciou as leis das órbitas planetárias, conjecturou que esse arranjo de densidade máxima seria um empilhamento conhecido como “cúbico de face centrada” (CFC). O próprio Kepler, porém, não foi capaz de provar esse palpite e passou a bola para outros matemáticos.
Acontece que o problema revelou-se mais difícil do que aparentava inicialmente. Quem conseguiu 
fazer essa demonstração, já no século 19, foi o grande matemático Karl Gauss. Na verdade, o que Gauss demonstrou foi que o arranjo CFC é o mais denso dos arranjos regulares. Em um arranjo regular, há uma periodicidade na disposição dos planos de esferas. A demonstração de Gauss, portanto, não inclui a possibilidade de haver um arranjo desordenado mais denso que o arranjo CFC.
Para visualizar o arranjo “cúbico de face centrada” (CFC) imagine um cubo e coloque uma esfera em cada vértice desse cubo. Depois, coloque uma esfera no centro de cada face do cubo. Todas as esferas devem ter o mesmo raio. Por fim, imagine que cada aresta do cubo vai encolhendo simultaneamente até que cada esfera encoste em outras vizinhas e o encolhimento não possa prosseguir. A figura abaixo mostra, à esquerda, a estrutura CFC antes do colapso das arestas do cubo. A figura à direita mostra a estrutura já compactada.
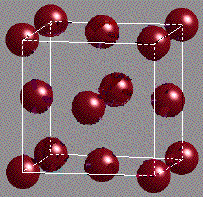
O arranjo CFC equivale, em densidade, a outro tipo de arranjo, chamado de “hexagonal compacto”, ou HCP. Ambos têm a mesma densidade (aproximadamente 74%) e um pode ser transformado no outro por um simples deslocamento dos planos de esferas. A receita para montar um arranjo de máxima densidade (CFC ou HCP) é bastante simples. Basta cumprir os seguintes passos:
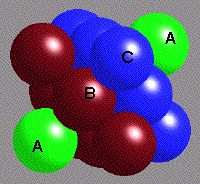
1) Forme a primeira camada sobre um plano horizontal cercando cada esfera com seis outras, todas encostadas compactamente. A figura A mostra como ficam as sete primeiras esferas dessa camada. A partir desse ponto, basta ir completando essa primeira camada. O arranjo obtido nessa camada forma hexágonos regulares em torno de cada esfera, como mostra a figura A.
2) A segunda camada é feita com esferas colocadas nas reentrâncias (espaços vazios) da 
primeira camada. A figura B mostra como são colocadas três esferas dessa segunda camada. A esferas da segunda camada foram pintadas de branco para melhor distingui-las das esferas da primeira camada.
3) Na terceira camada, temos duas possibilidades: uma resulta no arranjo CFC e a outra, no arranjo HCP. Elas são mostradas na figura C:
b) No primeiro caso, as esferas da terceira camada repousam nas reentrâncias da segunda, 
sobre os pontos vermelhos da figura. As esferas nesse arranjo, descrito como ABC, são localizadas nos círculos vermelhos. Esse é o arranjo da estrutura CFC.
a) Na outra possibilidade, a terceira camada é alinhada perfeitamente com a primeira. Esse arranjo, descrito como ABA, forma a estrutura HCP. Na figura C, as posições das esferas da terceira camada no arranjo HCP são indicadas por pontinhos azúis. As esferas não são mostradas na figura.
Um bom exercício de geometria espacial, que recomendamos, consiste em mostrar que a densidade dos arranjos CFC ou HCP vale:
Como dissemos antes, restava provar que os arranjos HCP e CFC são mais densos que qualquer arranjo, mesmo os aleatórios, sem ordem definida, conseguidos jogando as esferas ao acaso em uma caixa e chacoalhando a caixa. Pois bem, depois de inúmeras tentativas, essa prova foi finalmente obtida, em 1998, por Thomas Hales, da Universidade de Michigan. Novamente, como no caso do mapa de quatro cores, foi necessário apelar para computadores. A demonstração de Hales foi ainda mais elaborada que a dos pesquisadores de Illinois, usando uma série de programas com mais de 3 gigabytes de código.
Do mesmo modo que em relação à demonstração do mapa de quatro cores, muitos matemáticos continuam insatisfeitos e mantêm a esperança de que alguém, no futuro, consiga demonstrações formais, usando só a cabeça, papel e lápis.
Resta saber qual é a maior densidade que se pode conseguir com um arranjo aleatório das esferas. Esse problema ainda não foi resolvido mas há um consenso que deve valer por volta de 0,64. Além disso, hoje muita gente trabalha com variações desse problema incluindo esferas de raios variados. Essa é uma linha de pesquisa em plena atividade.
O último teorema de Fermat.
Esse, sem nenhuma dúvida, foi o problema mais famoso da Matemática, desde que foi enunciado no século 17.
Pierre de Fermat, acreditem, foi mais um advogado que ficou famoso como matemático amador. E tanto fez que é considerado como um dos maiores craques da teoria dos números. Para culminar, em toda sua vida só publicou um artigo, além do mais anonimamente, como apêndice do livro de um colega. Seu nome só não foi esquecido porque seu filho Samuel publicou, postumamente, sua enorme produção matemática contida na forma de cartas a amigos, anotações, artigos inéditos e notas rascunhadas em margens de livros.
Pois foi justamente em uma dessas notas, rabiscada na margem de uma cópia do livro Aritmetica, de Diofantos, que Fermat deu partida ao mais intrigante problema matemático dos últimos três séculos. A nota dizia:
“Uma equação do tipo xn + yn = zn, onde x, y, z e n são inteiros, não tem solução para valores de n maior que 2.”
Para dar mais mistério ao caso, Fermat acrescentou:
“Achei uma prova verdadeiramente notável desse teorema mas essa margem é muito pequena para contê-la”.
Os matemáticos, hoje em dia, acham que Fermat se enganou e logo descobriu que sua prova estava errada. Pois, se estivesse correta, ele a teria enviado em suas cartas aos colegas, como costumava fazer. Aliás, é curioso notar que, em todo seu extenso trabalho matemático, Fermat apenas enunciava os teoremas, todos muito importantes, sem demonstrá-los.
Voltando ao teorema acima: praticamente todo matemático, ilustre ou não, desde 1630 até hoje, gastou algum tempo tentando achar uma forma de demonstrá-lo. Gauss conseguiu prová-lo apenas para o caso de n = 4. Euler, um gênio sem limites, produziu uma prova que depois reconheceu como errônea. Vultosos prêmios foram oferecidos por várias instituições a quem conseguisse a proeza, o que motivou uma enxurrada de provas erradas.
Finalmente, em 1993, o matemático inglês Andrew Wiles apresentou uma demonstração que, aparentemente, 
resolvia o problema. Como previsto, essa demonstração era bastante complicada e não foi logo entendida pelos colegas. O próprio Wiles, logo após sua apresentação, descobriu falhas na demonstração e achou melhor retirá-la. Depois de trabalhar arduamente por mais um ano, em setembro de 1994, Wiles apresentou uma nova prova, mais simples que a primeira, que é considerada pela comunidade de matemáticos como correta. Até que enfim, depois de mais de três séculos infernizando a vida dos matemáticos, o último teorema de Fermat foi vencido.
Aos interessados em mais detalhes sobre os métodos usados por Wiles e em um relato da intensidade de seu envolvimento com o problema, recomendamos a leitura do excelente livro de Simon Singh, O Último Teorema de Fermat, que já foi traduzido para o português.
