Os Descendentes de ф
A querida mestra Dona Fifi chamou nossa atenção, numa de suas famosas apostilas (Veja O NÚMERO ф), para um número famoso, o número áureo ф. O número ф está intimamente ligado à geometria do pentágono, tem relação estreita com os conhecidos números de Fibonacci e é uma das raízes da equação
Ou seja, 
, com uma aproximação de seis casas decimais. A seqüência dos números de Fibonacci {1,1,2,3,5,8,13,…} ocorre naturalmente em muitos outros contextos, desde a geometria dos girassóis, a métrica de poemas, nas sinfonias, na arte antiga, nos computadores e até no sistema solar. A ligação direta de F com os números de Fibonacci é dada pela relação
onde ф(n) é o enésimo termo da seqüência.
Nessas notas estudaremos as soluções da equação 
, com k >2, usando o método de Newton. Para k=3, a solução é o chamado número plástico e as soluções que se seguem para k=3,4,5…, são como uma família, que informalmente, chamaremos de os descendentes de ф.
O número plástico.
O número plástico ou número de Padovan foi descoberto independentemente pelo arquiteto e monge beneditino Hans van der Laan (1904-1991) e por Gérard Cordonnier. Traduzindo e estudando o livro de Van der Laan, Architectonic Space, em 1983, o também arquiteto Richard Padovan descobriu uma seqüência de números inteiros onde a sua conexão com o número plástico apresenta um grande paralelo com o número de ouro e a seqüência de Fibbonacci. O número plástico é ainda pouco conhecido considerando suas virtudes como instrumento de desenho e é obtido como a solução real da equação cúbica:
e da equação: 
Para conhecermos o número plástico, portanto, precisamos aprender a resolver essas equações. Começaremos, na próxima seção, com a solução da equação cúbica na forma dada acima.
Solução da equação cúbica.
No seu famoso livro Ars Magna, publicado em 1545, ano que marca o início da matemática moderna, Girolamo Cardano (1501-1576) apresenta a solução da equação
.
Usando a notação atual, as soluções da equação acima são obtidas como se segue. Primeiro, verificamos o sinal do discriminante:
.
Se D>0, a equação tem uma raiz real e duas imaginárias. A raiz real é dada por
,
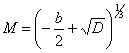onde
e
.
Por sua vez as duas raízes imaginárias são dadas por:
e
.
Se D = 0, existem três raízes reais e pelo menos duas são iguais. As raízes são dadas por:
e
.
Se D<0, o cálculo das raízes é simplificado usando-se a trigonometria:
,
,
,
onde
.
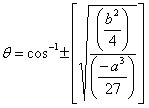Na equação acima, Q é em graus, o sinal (-) aplica-se quando b>0 e o sinal (+) quando b<0.
Aplicando os resultados expostos acima vamos resolver a equação . Fazendo a = b = -1, calculamos o discriminante e obtemos D = 0,212962963 > 0. Logo, a equação tem uma raiz real e duas raízes complexas conjugadas.
Usando as equações que dão M e N, determinamos a raiz real, x1 = p = 1,324717957, que é o número plástico com nove casas decimais.
No link abaixo, oferecemos, para download, um programa que calcula as raízes de uma equação cúbica completa, dados os 4 coeficientes reais a, b, c, d. Nesse programa, utilizamos exatamente o algoritmo descrito acima, devido a Cardano.
SOLUÇÃO DE UMA EQUAÇÃO CÚBICA do tipo a x3 + b x2 + c x + d = 0.
Equações com grau maior que 3 não têm solução analítica como essa que vimos para a equação cúbica. Para resolver uma equação como precisamos usar um método numérico. Um dos métodos mais poderosos que existem foi inventado por Isaac Newton e vamos descrevê-lo na próxima seção.
Solução numérica. O método de Newton.
No livro O Método de fluxos, escrito em 1671 por Isaac Newton (1642-1727), encontramos o método de Newton para a solução aproximada de equações. Se a equação a ser resolvida é f(x) = 0, estabelecemos um processo iterativo da seguinte maneira: assumindo um valor inicial x0 para a raiz desejada, calculamos um novo valor para a raiz, x,como se segue:
,
onde f´(x) é a derivada da função f(x). Obtido x, fazemos x=x0 e retornamos a equação acima, determinando um novo x. Calculamos a diferença x-x0 e notamos que essa diferença diminui a cada passo no processo. Prosseguindo iterativamente, podemos obter uma aproximação tão precisa quanto se queira. Como exemplo, vamos resolver a equação:
,
onde k é um número inteiro positivo. A derivada de f(x) é dada por: 
.
Escrevemos então,
.
Fazendo k=3, como ilustração, estabelecemos um processo iterativo para a determinação da raiz da equação que, como vimos, é o número p de Padovan. A equação acima torna-se,
.
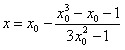De posse de uma calculadora de mão, ou ainda melhor, de um computador, iniciamos o processo iterativo. Fazendo inicialmente, x0=1,00, iteramos essa última equação. O resultado obtido a cada passo é mostrado na tabela 1, abaixo.
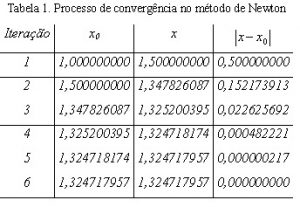
Podemos notar que, após cinco iterações, obtemos o valor da raiz com uma precisão de nove casas decimais, o que mostra a rápida convergência do método de Newton.
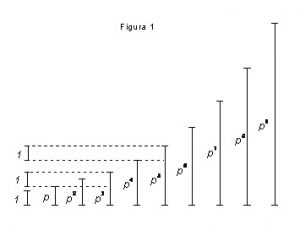
Na fig. 1, mostramos uma seqüência de medidas, iniciando com a unidade seguida de potências crescentes de p, até a potência 9. Podemos observar na figura que as equações e são satisfeitas pelas medidas, ou seja (p3 = p + 1) e (p5 = p4 + 1), como deveria ser.
Algebricamente podemos também ver que p é solução de , desde que,
.
Notamos que as 5 raízes da equação são as três raízes da equação e as duas raízes complexas da equação 
, 
e 
.
Na fig. 2 mostramos o gráfico das funções cujas raízes reais são idênticas e iguais a p, equações e , nomeadas respectivamente de u(x) e v(x).
Associada à seqüência de Fibonacci, Padovan introduziu uma série de números tal que o enésimo termo é dado por P(n+1) = P(n-1) + P(n-2) com P(0)= P(1)=P(2)=1. A série é tal que:
.
O matemático francês Édouard Lucas, em 1876, estudou uma seqüência com a mesma regra de formação dos números de Padovan, mas usando diferentes valores iniciais. Em 1899, R. Perrin aprofundou as idéias de Lucas e hoje a seqüência A(n) é conhecida como a seqüência de Perrin. Os números de Perrin diferem dos P(n) pelo fato de A(0) = 3, A(1) = 0 e A(2) =2. Na tabela 2, nas colunas 2 e 3, mostramos alguns valores das seqüências P(n) e A(n).
Podemos notar que a razão de números de Perrin consecutivos tende a p, por exemplo, 
. Lucas percebeu uma propriedade sutil dos números de Perrin. Sempre que n é um número primo (um número que não é divisível por nenhum número além de si mesmo e 1), n divide A(n) exatamente. Por exemplo, sabemos que 11 é primo. Observando a tabela 2, A(11)/11 = 22/11 = 2. De maneira semelhante, 17 é primo, A(17)/17 = 119/17 = 7. Mais um exemplo, 43 é primo, A(43)/43 = 178364/43 = 4148. Esta propriedade apresenta uma maneira original de testar se um número é composto, ou seja, se não é primo. Por exemplo, quando n = 20, temos A(20)/20 = 277/20 = 13,85, que não é um inteiro. Portanto, 20 deve ser composto. Podemos então usar os números de Perrin para estabelecer se um número é primo ou não: qualquer número n que não divide A(n) é composto. Em 1982, Jeffrey Shallit da Universidade de Waterloo encontrou dois números compostos, 27141 e 904631, que dividem o número de Perrin correspondente. Em 1991, Steven Arno provou que os pseudo primos de Perrin devem ter, no mínimo, 15 dígitos. Um teste mais complicado para descobrir se um número é primo, baseado em vários números de Perrin sucessivos, foi estudado e até o momento não se conhecem exceções.
O número F teve uma importância fundamental na idade média nas construções de catedrais e obras de arte, onde a proporção áurea era usada extensivamente por arquitetos e artistas. Muitas catedrais famosas foram erguidas com suas formas regidas pelo número F. Na figura 3 ilustramos uma aplicação do número plástico p. Mostramos a foto da abadia de “Sint Benedictusberg” em Vaals, Holanda, extraída do artigo “Morphic Numbers” de J. Aarts,J. R. Fokkink, e G. Kruijtzer, Nieuw Arch. Wisk 5-2, 56-58, 2001, que foi construída seguindo as proporções regidas pelo número p.
Figura 3. Interior da igreja da abadia “Sint Benedictusberg em Vaals, Holanda, construída seguindo os princípios arquiteturais de Dom Van der Laan baseados no número plástico p.
http://www.math.leidenuniv.nl/~naw/serie5/deel02/mrt2001/pdf/archi.pdf
Outras soluções da equação xk-x-1=0, k>3
Usando o método de Newton podemos encontrar outras soluções da equação acima, com k>3. Podemos pesquisar as seqüências numéricas correspondentes aos números de Fibonacci e Padovan. Na tabela 3 dispomos algumas soluções obtidas dessa equação.
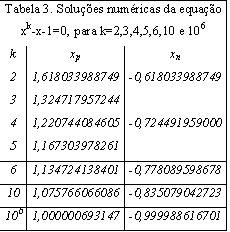
Podemos notar que, para k par, existem duas soluções reais, uma positiva e outra negativa. Para k ímpar, existe somente uma solução real.
Nas figuras 3 e 4 mostramos várias raízes positivas e negativas mostrando que quando 
a raiz positiva 
e a raiz negativa 
.
Na figura 5 ilustramos a presença de duas raízes reais quando k é par e de uma raiz real quando k é impar, para k=2,3,4 e 5.
Na tabela 4 mostramos a lei de formação das sequências numéricas associadas às soluções da equação (18) com k=2,3,4,5.
Na figura 6 mostramos a convergência da razão dos termos consecutivos das seqüências associadas às soluções da equação com k=2,3,4,5.
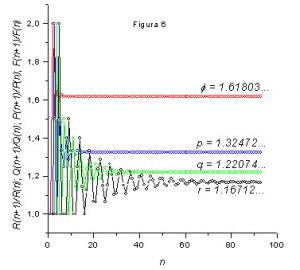
Observando a figura 6 podemos notar que quanto maior é k mais lenta é a convergência da razão entre termos subseqüentes das seqüências em direção à raiz positiva associada. Compare com os resultados da tabela 3.
π, ф, p e os fractais.
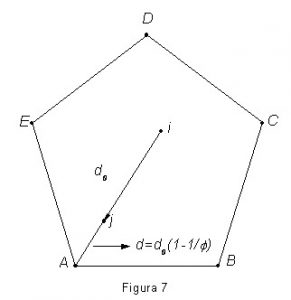
Procedendo de maneira similar àquela descrita no artigo Quarenta séculos de π para a construção do triângulo de Sierpinski, usamos os dígitos decimais de π para gerar números inteiros aleatórios de 0 a 9. Na figura 7 temos um pentágono ABCD, eqüilátero de lado unitário. De posse dos dígitos decimais de π procedemos da seguinte maneira: ao vértice A associamos os números 0 e 1, ao vértice B associamos os números 2 e 3, ao vértice C associamos os números 4 e 5, ao vértice D associamos os números 6 e 7 e ao vértice E associamos os números 8 e 9. Geramos no plano um ponto qualquer i, veja a figura 7, e procedemos a uma leitura sequencial dos dígitos de p. Se por exemplo, o dígito lido é 0 ou 1, movemos o ponto i para j ao longo da linha que une o vértice A ao ponto i, de modo que a distância do ponto j ao vértice A é agora, 
, onde F é o número de ouro. Gravamos o ponto j e lemos o dígito seguinte de π e procedemos da mesma maneira em relação ao novo vértice escolhido e fazendo i=j.
O resultado desse processo para 100000 dígitos de π lidos é mostrado na figura 8.
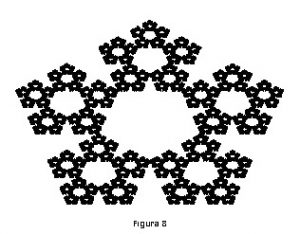
O fractal da figura 8 foi originalmente obtido por Jeff Cameron, usando um programa e um conjunto de números aleatórios diferentes, e nomeou-o de “The military Gasket”.
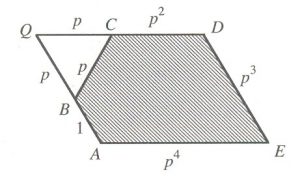
Midhat J. Gazalé, no seu excelente livro, Gnomon: from Pharaohs to Fractals, introduz o pentágono de prata. Na figura 9 mostramos o paralelogramo ABCDE. Os lados AB, BC, CD, DE, EA, são iguais a 1, p, p2, p3 e p4, respectivamente. O ângulo AED é igual a 60o.
Prolongando os lados AB e CD eles se interceptam em Q. Podemos então observar que, na figura, DE=AB+BQ, ou seja, p3=p+1, e que AE=QC+CD ou p4=p2+p, onde p é o número de Padovan.
Se adicionarmos o triângulo eqüilátero AEF, veja a figura 10, obtemos o paralelogramo BCDEF, cujos lados BC, CD, DE, EF e FB, são iguais a p, p2, p3, p4 e p5, respectivamente. Este é o pentágono de prata.
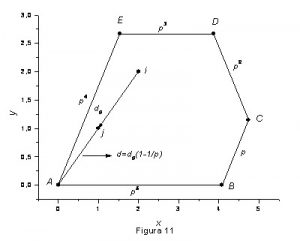
Tomando o pentágono de prata mostrado na figura 11, aplicamos o mesmo algoritmo usado na construção do fractal da figura 8, só que agora as distâncias seguem a regra, 
, onde p é o número plástico.
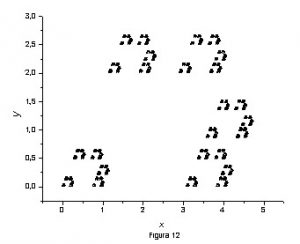
Para nossa surpresa, obtivemos um fractal regular mostrado na figura 12.
Nas proximidades de cada vértice temos uma cópia da figura maior caracterizando a autosimilaridade. Na figura 13 mostramos uma janela da figura 12, proximidades do vértice A, ilustrando essa propriedade dos fractais regulares.
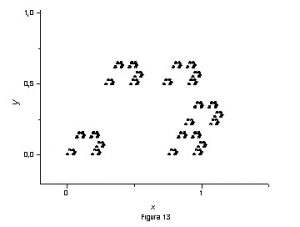
Mantivemos os eixos coordenados para que o leitor possa notar a diferença de escala entre a figura 12 e a figura 13.
Concluindo, gostaria de acentuar que, com um computador pessoal, o leitor interessado pode pesquisar outras soluções e as seqüências numéricas associadas, da equação xk-x-1=0 e, quem sabe, descobrir novas propriedades dos descendentes de F
J. Maurício O. Matos é físico e professor da UFC.
Referências
1. What is Mathematics, Richard Courant and Herbert Robbins, revised by Ian Stewart, Oxford University Press, 1996.
2. História da Matemática, Carl B. Boyer, Editora Edgard Blücher Ltda., 1996.
3. Mania de Matemática, Ian Stewart, Jorge Zahar Editor, 2004.
4. Fascinating Fibonaccis, Trudi Hammel Garland, Dale Seymour Publications, 1987.
5. Proportion: Science, Philosophy Architecture, Richard Padovan, Spon Press, 1999.
6. Handbook of Mathematical Functions, Edited by Milton Abramowitz and Irene A. Stegun, Dover Publications, INC., 1965.
7. The Divine Proportion, H. E. Huntley, Dover Publications, INC., 1970.
8. Fractals, Chaos, Power Laws, Manfred Schroeder, W. H. Freeman and Company, 1991.
9. Gnomon from Pharaohs to Fractals, Midhat J. Gazalé, Princeton University Press, 1999.
