Apostilas sobre a curvatura de Gauss.
Leonhard Euler (pronuncia-se “Óiler”) viveu apenas 76 anos, de 1707 a 1783; Carl Gauss viveu um pouco mais, 78 anos, de 1777 a 1855. Eles foram dois dos maiores (ou talvez “os maiores”) gênios matemáticos que já passaram por esse pálido ponto azul.
NOTA do EDITOR: Veja a seção TRÊS GRANDES MATEMÁTICOS que trata de Euler, Gauss e Galois.
Nessas apostilas vou falar de dois ramos da Matemática que, praticamente, foram criados por esses caras: a “geometria diferencial” e a “topologia”.
A geometria diferencial, como o nome sugere, usa os poderes do cálculo diferencial para estudar curvas e superfícies. A topologia se interessa pela “forma” dos objetos geométricos sem levar em conta suas medidas. Não tenho a menor intenção de entrar nos detalhes técnicos desses brinquedos dos matemáticos. Quero apenas dar uma pálida idéia (pálida, loira, de tranças e olhos azúis…) de alguns notáveis resultados obtidos por Euler e Gauss e salientar como esses dois ramos inaugurados por eles estão inesperadamente ligados entre si. Em particular, vou falar sobre a “curvatura de Gauss” pois essa curvatura serviu de lastro para trabalhos posteriores de outros matemáticos e foram aproveitados por Einstein em sua Teoria da Relatividade Geral.
Meu propósito é apenas divertir e, quem sabe, motivar algum futuro Gauss ou Euler brasileiro, ao mesmo tempo que faço passar o tempo (já tão curto) que me resta nesse vale de sorrisos.
1 – O que é a curvatura.
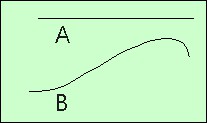 O que faz a reta (A) ao lado ser diferente da outra curva (B)? É fácil: a curva (B) é “encurvada” e a reta não é. A curva (B) deve ter alguma propriedade que a reta não tem. Você adivinhou, essa propriedade é a curvatura. A reta tem curvatura zero e a curva tem curvatura diferente de zero. Só falta achar um jeito de medir essa curvatura, dar a ela uma noção mais precisa e válida para qualquer ponto de qualquer curva.
O que faz a reta (A) ao lado ser diferente da outra curva (B)? É fácil: a curva (B) é “encurvada” e a reta não é. A curva (B) deve ter alguma propriedade que a reta não tem. Você adivinhou, essa propriedade é a curvatura. A reta tem curvatura zero e a curva tem curvatura diferente de zero. Só falta achar um jeito de medir essa curvatura, dar a ela uma noção mais precisa e válida para qualquer ponto de qualquer curva.
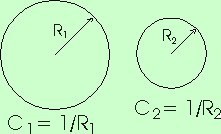
Existe uma curva muito simples e bela cuja curvatura é obviamente igual em todos seus pontos: a circunferência. Vamos, então, dar um valor para a curvatura da circunferência. Como também é evidente que uma circunferência menor é mais encurvada que outra maior, fica claro que a curvatura deve ser inversamente proporcional ao raio. Isto é, a curvatura C de uma circunferência de raio R será dada por C = 1 / R. Quanto maior o raio, menor a curvatura.

Muito bem, sabemos medir a curvatura da circunferência. Mas, e se a curva for mais variada, como essa aí em cima? É claro que essa curva não tem curvatura constante; no lado esquerdo a curvatura deve maior que no lado direito. Temos, portanto, de achar um jeito de saber a curvatura em cada um dos pontos da curva, já que ela não é constante. Para isso, apelaremos para a curvatura da circunferência (C = 1/R).
Para achar a curvatura da curva em um ponto P faremos o seguinte: desenhamos uma circunferência no lado côncavo da curva de tal modo que o único ponto em comum entre a curva e a circunferência seja o próprio ponto P. Provavelmente existem várias circunferências com essa característica mas tomamos aquela que tem o maior raio possível. O matemático que deu um nome a essa circunferência (parece que foi Leibnitz) devia estar apaixonado pois chamou-a de “círculo osculante”, isto é, o círculo que beija a curva. Lindo nome.
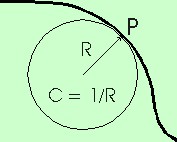
Desse modo, a curvatura da curva no ponto P será igual à curvatura do círculo osculante nesse mesmo ponto onde se beijam. No caso da figura ao lado, será C = 1 / R, pois R é o raio do círculo osculante.
Como a curvatura é o inverso do raio, a unidade de curvatura é o inverso do metro e se chama dioptria. Essa dioptria é o popular “grau” dos óculos (1 grau = 1 dioptria). Por exemplo, uma lente de óculos com 0,5 graus, ou 0,5 dioptrias, tem raio de curvatura igual a 2 metros. Aliás, Gauss também deu importantes contribuições à óptica, tendo até escrito um livro intitulado “Investigações Dióptricas”.
E se, em vez de uma curva, tivermos uma superfície – como medir sua curvatura? Essa superfície vista ao lado, uma chapa de metal, por exemplo, está claramente encurvada, logo, queremos determinar uma curvatura em cada ponto dela. Será que existe uma “esfera osculante” cujo raio é o inverso da curvatura? Veja no próximo episódio.
2 – A curvatura de uma superfície.
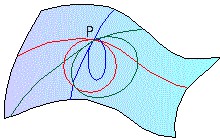
Resposta para a pergunta do capítulo anterior: não. O motivo de não podermos usar uma esfera osculante para medir a curvatura de uma superfície é fácil de ser entendido. Considere um ponto P qualquer da superfície. Por esse ponto passa uma infinidade de curvas diferentes e cada uma delas tem um círculo osculante próprio e, portanto, uma curvatura diferente das demais. Uma esfera osculante teria o mesmo raio que algum desses círculos osculantes. Mas, qual deles seria o escolhido? Essa ambiguidade na escolha mostra que temos de achar outra forma de definir a curvatura em um ponto da superfície curva.
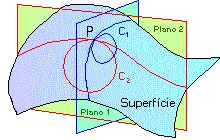
Vejamos como é definida a curvatura de Gauss em um ponto P qualquer da superfície. Fazemos um plano cortar a superfície no ponto P. A interseção do plano com a superfície é uma curva. Achamos a curvatura dessa curva desenhando o círculo osculante à curva que está contido no plano. Vamos então testando vários planos até que achamos aquele que contém o menor círculo osculante possível, isto é, aquele que tem o menor raio. No desenho ao lado, vamos supor que esse plano seja o Plano 1. Portanto, a curva azul será a curva de maior curvatura entre aquelas que estão na superfície e que passam por P. Repetimos o processo até achar a curva de menor curvatura, no desenho representada em vermelho. Digamos, então, que a curvatura máxima seja C1 e a curvatura mínima seja C2. Pois bem, a curvatura de Gauss no ponto P será, pura e simplesmente, o produto das curvaturas C1 e C2. Isto é:
C = curvatura de Gauss = C1 x C2.
Desse modo, podemos achar a curvatura de Gauss em qualquer ponto da superfície. Por exemplo, se a superfície for um plano, todas as interseções de planos que passam por P serão retas, logo, terão curvatura nula. Portanto, o plano tem curvatura de Gauss nula.
A curvatura de Gauss pode ser positiva, negativa ou nula. Será positiva se as curvas de máxima e mínima curvatura forem encurvadas para o mesmo lado. Nesse caso, os dois círculos osculantes ficam no mesmo lado da superfície. Esse é o caso da superfície (A) vista abaixo. Será negativa se uma curva for encurvada para um lado e a outra, para o outro. Isto é, se os círculos osculantes ficam em lados opostos. É o caso da superfície (B), que parece uma sela. E é nula se pelo menos uma das curvas for reta, isto é, tiver curvatura zero. É o caso do cilindro (C), na figura. E é o caso também da chapa de metal mostrada na apostila anterior.

A grande vantagem dessa curvatura de Gauss, além da simplicidade da definição, é a seguinte: ela pode ser observada e medida sem precisar apelar para os círculos osculantes fora da superfície. Isto é, ela pode ser medida sem sair da própria superfície. É claro que isso implica em outra forma de definí-la, como veremos a seguir.
3 – Como saber se o espaço é curvo.
Gauss mostrou que a curvatura de uma superfície é uma propriedade intrínseca. Isso quer dizer que é possível saber se o espaço onde se vive é curvo ou plano sem precisar sair dele, apelando para alguma dimensão extra. Em outras palavras, os círculos osculantes usados anteriormente para definir a curvatura e que estão fora da superfície são desnecessários para se medir a curvatura. Gauss mostrou isso em um teorema e ficou tão orgulhoso de seu resultado que chamou o teorema de “Teorema Egregium”, que aqui em Sobral seria traduzido como “Teorema Arretado”. A demonstração desse teorema é muito técnica para ser mostrada aqui, mas, podemos ilustrar seu significado com exemplos visuais.
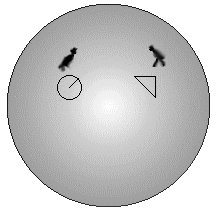
Imagine uma civilização de seres bidimensionais (os chatóides) que habitam uma enorme superfície esférica.
Confinados em seu espaço, os chatóides ignoram a existência de outra dimensão que nós, seres tridimensionais, sabemos existir. Os chatóides descobriram um grande número de propriedades geométricas em seu espaço e sabem fazer medidas de distâncias, ângulos e áreas. Por exemplo, desenhando três segmentos de reta que formam um triângulo eles verificam que a soma dos ângulos internos é 180° (ou π).
E dividindo o comprimento de uma circunferência por seu raio eles acham 2π. Assim, os geômetras chatóides concluem: “ao que parece, vivemos em um espaço plano”.
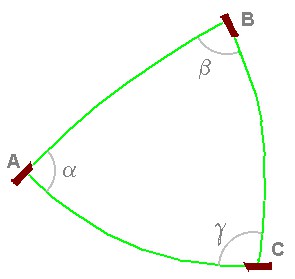
Entretanto, com o desenvolvimento da tecnologia chatóide, eles começam a explorar o universo onde vivem, indo cada vez mais longe. E repetem suas medidas, só que agora com triângulos e circunferências cada vez maiores. Por exemplo, três astronautas chatóides formam um enorme triângulo enviando feixes de laser uns aos outros. Nada mais reto que um raio de luz, dizem os chatóides. Cada qual mede o ângulo entre o feixe que enviou e o que recebeu. Quando se reunem para comparar suas medidas têm uma surpresa: a soma dos três ângulos é maior que 180°! Desconfiando da qualidade da luz de seus lasers, usam cabos bem esticados entre três pontos fixos muito distantes uns dos outros e chegam ao mesmo resultado. Nesse ponto, eles começam a achar que o espaço onde vivem não é plano. Na verdade, eles podem até calcular qual é a curvatura do espaço, usando a soma dos ângulos que obtiveram.
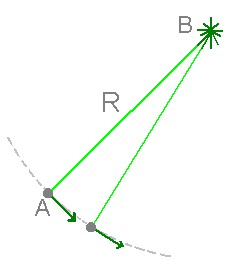
Em outra experiência eles traçam uma grande circunferência: um astronauta A vai a uma grande distância R da base B mantendo um enorme cabo esticado. Deslocando-se sempre perpendicularmente ao cabo esticado, percorre uma gigantesca circunferência com centro em B. Depois, dividindo o comprimento do perímetro L pelo raio R eles acham, como já desconfiavam, um valor menor que 2π. Com seus conhecimentos avançados de geometria não-Euclideana, os chatóides reconhecem que moram em um espaço curvo e calculam a curvatura de Gauss desse espaço.
Nós vivemos em um espaço tridimensional. Será que nosso espaço é curvo? Ora, dirá você, basta fazer um enorme triângulo de feixes de laser e verificar se a soma dos ângulos é igual, maior ou menor que 180°. Infelizmente, nossa tecnologia é inferior à tecnologia dos chatóides e não sabemos ainda se nosso universo é plano ou curvo. Boa parte dos cosmologistas acha que é plano mas, por enquanto, isso não está inteiramente comprovado. Em outra ocasião poderemos conversar mais sobre a curvatura do universo.
Experiências como essas descritas acima podem mostrar se o espaço é curvo ou não e são suficientes para medir a curvatura sem apelar para uma dimensão extra. O “teorema arretado” de Gauss mostra como isso é feito. Como disse antes, não estou a fim de entrar nessas minúcias técnicas, mas, ainda quero mostrar a vocês um bocado de resultados bem divertidos, relacionados com a curvatura de Gauss e com um número inventado por Euler. O melhor está por vir.
NOTA do EDITOR: Embora a autora evite usar fórmulas mais complicadas em seu texto, damos abaixo, em benefício de leitores com gosto para a matemática, a definição da curvatura de Gauss em um ponto P de uma superfície, usando a medida do raio R e do perímetro L(R) de uma circunferência desenhada sobre a superfície:
![]()
Se a superfície for plana, a curvatura é zero pois L(R) = 2πR. Se for esférica, o limite dá uma curvatura constante, igual a 1/R.
4 – A curvatura de Gauss em uma superfície.
A curvatura de Gauss descrita na apostila anterior é local, isto é, vale para um ponto da superfície. Mas, queremos saber, também, como medir a curvatura de toda a superfície ou, pelo menos, de uma parte dela. Veremos agora como fazer uma medida dessas. Só assim poderemos falar da curvatura do espaço em que vivemos, como um todo. Talvez até medir a curvatura de todo o universo.
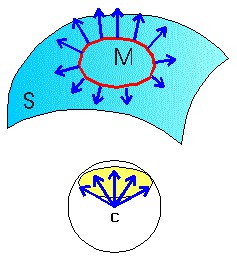
Imagine uma superfície qualquer S que não tenha furos. Trace, sobre ela, uma curva que delimita uma região fechada M na superfície. Vamos mostrar como calcular a curvatura de Gauss dessa região. Em cada um dos pontos da curva que contorna M imagine uma seta perpendicular à superfície nesse ponto. Essas setas deverão ter comprimento igual a 1 e, sendo a superfície curva, apontarão para direções variadas. Se você quiser, pode chamar cada seta dessas de vetor normal. Agora, faça o seguinte (mentalmente): pegue todas as setas e junte-as pelas extremidades em um único ponto C do espaço. Você terá formado um “buquê” de setas. E como todas têm o mesmo comprimento unitário, suas pontas estarão sobre uma parte da superfície de uma esfera de raio unitário que é mostrada com cor amarela na figura. Em termos mais técnicos, fizemos um mapeamento da região M sobre a esfera unitária. Aliás, foi estudando mapas e globos terrestres que Gauss começou tudo isso.
Pois bem: Gauss mostrou que o valor da área dessa região amarela mede a curvatura da região M da superfície curva. Veja que estamos falando de curvatura de toda uma região e não apenas de um ponto da superfície. Com essa definição, poderemos achar a curvatura total de qualquer superfície, aberta ou fechada.
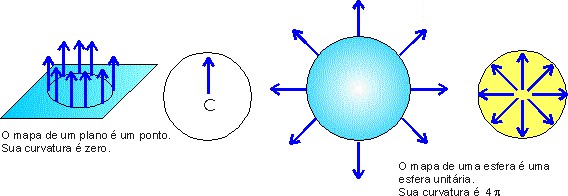
Vejamos dois exemplos simples: um plano (superfície aberta) e uma esfera (superfície fechada). Traçando qualquer curva sobre o plano e juntando todas as setas normais no centro da esfera unitária o resultado é apenas um ponto nessa esfera unitária. Isto é, a região “mapeia” sobre um único ponto na esfera unitária (o “buquê” é só uma haste). E, como um ponto não tem área, isso significa que a curvatura do plano é zero, o que já sabemos de longas datas. Na outra figura, vemos que todos os vetores normais à superfície da esfera “mapeiam” sobre toda a superfície da esfera unitária. Portanto, como a área da esfera unitária é
4π (1)² = 4π, essa é a curvatura total da esfera (qualquer esfera).
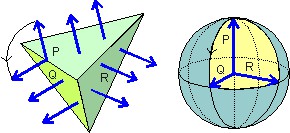
É moleza achar a curvatura de planos e esferas. Vamos ver, agora, como resolver casos mais elaborados usando esse processo de mapeamento sobre uma superfície que tem “bicos” ou “vértices”. A superfície que vamos usar é uma pirâmide com três lados mutuamente perpendiculares, como visto na figura. Todas as setas apoiadas na face P “mapeiam” em um único ponto (P) sobre a esfera unitária. Do mesmo modo, as setas sobre o lado R mapeiam no ponto R e as setas no lado Q, no ponto Q.
Mas, ao passar por uma aresta uma seta faz um giro de 90° e o mapeamento desses giros sobre a esfera unitária são os arcos que vão de P a Q , de P a R e de R a Q. Portanto, segundo Gauss, a curvatura da superfície da pirâmide é a área amarela vista na figura da esfera unitária. Essa área, como é fácil de ver, mede 1/8 da área total da esfera unitária, logo, vale 4π/8 = π/2.
Portanto, qualquer vértice, ou bico, entre três superfícies mutuamente perpendiculares tem curvatura π/2. Esse é o caso de qualquer um dos 8 vértices do cubo. Logo, a curvatura do cubo é 8 x π/2 = 4π . Isto é, o cubo tem a mesma curvatura que a esfera, embora a esfera seja toda gordinha e o cubo todo quadradão. Os matemáticos dizem que ambos pertencem à mesma tradicional família topológica. Se você quer se exercitar nessa matéria, mostre que o mesmo é verdade para qualquer poliedro regular (tetraedro, dodecaedro etc).
Bem, essa história de família topológica é a dica para nosso tema da próxima apostila. Veremos como o trabalho de Gauss se entrelaçou de forma inesperada com os achados do grande matemático Euler.
5 – O número de Euler e a topologia.

O grande matemático Leonhard Euler foi, para todos os efeitos, quem inaugurou um ramo da matemática chamado topologia. Vamos agora falar de um dos teoremas topológicos de Euler.
NOTA DO EDITOR: Veja em <TRÊS GRANDES MATEMÁTICOS mais informações sobre Euler e a topologia.
Considere um objeto tridimensional bem simples: um cubo. O cubo tem 6 faces, 12 arestas e 8 vértices. Vamos chamar o número de faces de F, o número de arestas de A e o número de vértices de V (muito imaginativo…).
Euler inventou um número, que chamamos de número de Euler (E), definido assim:
E = F – A + V.
Portanto, o número de Euler do cubo é:
E(cubo) = 6 – 12 + 8 = 2.
O teorema de Euler diz que o número de Euler é constante para uma superfície qualquer. Isso quer dizer o seguinte: suponha que você divide cada face do cubo em 4 partes, traçando 2 segmentos de reta perpendiculares entre si, como vemos na figura. Agora, pontos como (A) ou (B) serão considerados novos vértices, linhas como (AB) serão novas arestas e áreas como (ABCD), novas faces. Pois conte (CONTE!) os novos números de faces, arestas e vértice. Você obterá: F´ = 24, A´ = 48 e V´ = 26. E, terá:
E´ = F´ – A´ + V´= 24 – 48 + 26 = 2 = E.
O resultado é o mesmo de antes. Pois acredite: mesmo se você desenhar linhas malucas sobre o cubo, criando uma porção de novas arestas, vértices e faces, obterá sempre o mesmo número de Euler: 2.
Acho que ninguém vai se admirar, a essa altura, ao constatar que o número de Euler continuará o mesmo até quando o cubo for deformado como mostra a figura. E a deformação pode ser tal que o cubo acabe virando uma jeitosa esfera (mudança de sexo) ou mesmo uma batata toda encalombada.
Tecnicamente, diz-se que o cubo, a esfera e a batata são todas superfícies topologicamente idênticas. Todas têm o mesmo número de Euler: 2.
Imagine que o cubo é feito de massa de moldar, dessa que as crianças adoram. Com jeito, é possivel transformá-lo em uma esfera, uma pirâmide ou uma batata doida sem rasgar nem cortar nada. Isso só é possível com objetos topologicamente iguais.
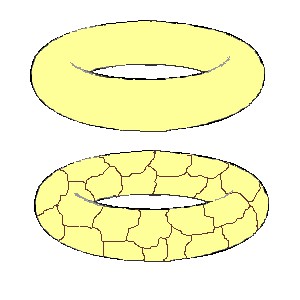
A coisa muda se o objeto tiver um furo. O objeto furado mais amado pelos matemáticos é o toro, essa coisa com forma de rosquinha do Piaui que vemos na figura ao lado. (Talvez essa minha opinião sobre os matemáticos seja um pouco exagerada…)
Se a gente fizer sobre a superfície do toro o mesmo que fizemos sobre a superfície do cubo (traçando linhas que formam faces, arestas e vértices) e depois fizermos as contas, acharemos um número de Euler nulo! Isto é: E(toro) = 0.
O toro, e qualquer superfície com um furo, é topologicamente diferente do cubo e da esfera. Não dá para transformar uma esfera de massa em um toro sem cortar ou rasgar alguma coisa.
Talvez você tenha estranhado que o toro tenha curvatura zero, quando ele nos parece bem encurvadinho.
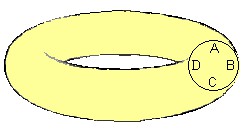
É óbvio que a curvatura local do toro não é zero em todos os pontos. O que é zero é a curvatura total do toro. Considere um corte no toro resultando no círculo ABCD. Os pontos que ficam no lado de fora (ABC), menos os extremos A e C, têm curvatura positiva. Os pontos que ficam no lado de dentro (ADC) têm curvatura negativa. E os pontos A e C têm curvatura nula. Computando tudo, achamos a curvatura total zero.
Quando a superfície tem buracos a expressão para o número de Euler fica sendo:
E = F – A + V = 2 – 2 x B,
sendo B o número de buracos ou furos na superfície. Para uma esfera ou um cubo, B = 0, logo, E = 2. Para o toro, B = 1, logo, E = 0. Com mais de um buraco, o número de Euler fica negativo.
E qual é a relação entre o número de Euler e a curvatura de Gauss? É o que veremos na próxima apostila.
6 – O teorema de Gauss-Bonnet.
A curvatura de Gauss (G) e o número de Euler (E) estão ligados pelo conhecido Teorema de Gauss-Bonnet, que diz:
G = 2π E = 2π (2 – 2 . B) .
Como você deve lembrar, B é o número de buracos na superfície. Para uma esfera, B = 0, logo, E = 2 e G = 4π . Para o toro, B = 1, logo E = 0 e G = 0.
A maravilha desse teorema é que ele liga uma propriedade geométrica, a curvatura de Gauss, com uma propriedade topológica, o número de Euler. E tudo de uma forma muito simples.
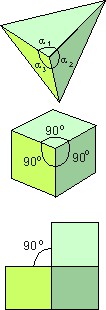
Para melhor apreciar o significado desse teorema vamos voltar à pirâmide de três faces. Primeiro, medimos os três ângulos das face com um transferidor e somamos os três. Depois, calculamos quanto falta a essa soma para completar 360°. Esse valor será chamado de “ângulo faltante”. Isto é, o ângulo faltante no vértice da pirâmide é Δ = 360 – (α1 + α2 + α3).
Se a gente fizer isso no vértice de um cubo, vamos achar Δ = 360 – (90 + 90 + 90) = 90° = π/2.
Esse resultado para o ângulo faltante no vértice do cubo fica mais claro se você cortar uma aresta e espalhar os três lados sobre uma mesa, como mostra a figura.
Portanto, o ângulo faltante em cada vértice do cubo é π/2. O ângulo faltante total (que chamaremos de T), para o cubo, será, portanto: 8 x π/2 = 4π . Esse valor, como já sabemos, mede a curvatura de Gauss do cubo! E isso vale não apenas para o cubo: vale para qualquer objeto geométrico. Portanto, o teorema de Gauss-Bonnet pode ser resumido como:
O ângulo faltante de uma superfície é igual à curvatura de Gauss dessa superfície.
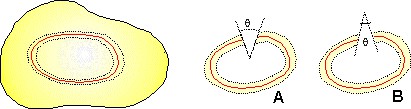
Usando o teorema de Gauss-Bonnet podemos medir experimentalmente a curvatura de Gauss de qualquer parte de qualquer superfície. Digamos, por exemplo, que queremos medir a curvatura de uma parte da superfície de uma batata. Fazemos o seguinte: traçamos, com uma caneta, uma curva sobre a casca da batata. Depois, com a ponta de uma faquinha bem afiada, cortamos a casca em torno da curva formando uma tira, como mostram as linhas pontilhadas. Puxamos a tira com muito cuidado para não rasgar, cortamos em qualquer ponto e apoiamos sobre a superfície de uma mesa plana. É provável que as pontas da tira não fechem, fazendo um ângulo que medimos com um transferidor. Esse é o ângulo faltante da superfície da batata contida dentro da curva. Logo, pelo teorema que acabamos de aprender, esse ângulo mede a curvatura dessa parte da batata. Se o ângulo for como visto na figura (A), a curvatura é positiva. Se for como na figura (B), é negativa. Se as pontas fecharem, a curvatura é nula. Isso acontece se fizermos o mesmo procedimento em uma superfície plana.
Bem, isso encerra nosso passeio pela geometria de Gauss e a topologia de Euler. Resta dizer que, muitos anos depois, esses belos achados foram ( e continuam sendo) usados pelos físicos no estudo da curvatura do nosso espaço tridimensional. Einstein mostrou que essa curvatura depende da quantidade de matéria e energia que está presente nesse espaço. Perto de uma grande estrela, como o nosso velho Sol, por exemplo, a massa encurva o espaço e um raio de luz que passe por ali será desviado. Isso foi comprovado, experimentalmente, aqui mesmo em Sobral, onde estou nesse momento. E eu tive o privilégio de presenciar esse momentoso evento, levada pela mão de meu saudoso pai. Mas, essa é outra história que posso contar noutra ocasião.

