Apostilas sobre o número Ф e a série de Fibonacci.
Nessas apostilas, Dona Fifi vai falar de um curioso número, o numero Ф, conhecido desde os tempos do patriarca da geometria, Euclides de Alexandria. Como ela nos mostra, esse número, e sua geratriz, a série de Fibonacci, além de suas intrigantes propriedades matemáticas surgem, inesperadamente, em várias manifestações naturais, talvez até nas mais intricadas configurações de nosso cérebro.
Como o número Ф é definido.
Nessas apostilas, tratarei de um número famoso desde os tempos de Euclides de Alexandria, patriarca da geometria que viveu por volta do ano 300 antes de Cristo. Esse número, chamado de F, foi definido por Euclides como resultado de uma operação geométrica muito simples.
Tome um segmento de reta AB e encontre um ponto intermediário, C, tal que AC/CB = AB/AC.
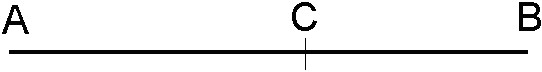
Pois bem, essa razão é o número Ф que vale:
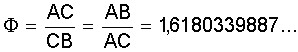
Definido assim, o número Ф costuma ser chamado de “proporção áurea”, um número de ouro que surge, como veremos, onde menos se espera, na matemática, na física, na biologia, nas artes e até nas conspirações esotéricas.
Vamos, para começar, examinar algumas propriedades do número Ф e mostrar como obtê-lo por operações algébricas simples. Observe que, se considerarmos que o segmento CB é igual a 1 e que o segmento AC vale x, temos, por construção:
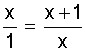Isto é, 
Como toda equação de segundo grau, esta tem duas soluções que são:
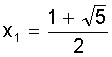e 
É 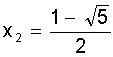claro que a solução positiva, x1, é justamente o número Ф, a “proporção áurea”. O negativo da outra solução será chamado de ф. Portanto:
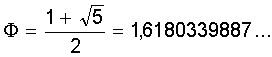e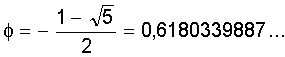 
Pronto, o número Ф está devidamente definido. Agora, vamos ver que ele surge como resultado de operações sobre uma simpática série inventada por um simpático italiano.
A série de Fibonacci.
Agora vou falar de algo que foi descoberto séculos após Euclides por um matemático chamado Leonardo que, sendo morador de Pisa, a cidade onde existe a famosa torre inclinada, era conhecido como Leonardo de Pisa. E, como nascera de família de boa estirpe, ficou também conhecido como Fibonaccci, que significa, literalmente, “filho de boa gente”.
Pois esse Fibonacci publicou, em 1202, um livro chamado “Livro dos Ábacos” onde tratava de vários temas matemáticos que considerava como importantes. Um deles, provavelmente inventado por ele próprio, tratava do problema de calcular quantos coelhos poderiam ser produzidos em um ano, a partir de um único casal. Da forma como enunciado por Fibonacci, o problema é muito artificial. Supõe que cada casal leva um mês, após nascer, para ficar fértil, gera sempre outro casal, a cada mês, e nenhum coelho morre durante o ano. Mas, o que interessa é o resultado.
O mês inicial (0) é usado para que o primeiro casal atinja a fertilidade. No mês seguinte o casal está fértil e um novo casal é gerado. Portanto, durante o segundo mês, teremos dois casais, o original (o X na figura indica um casal fértil) e o novo (representado por uma cruz), ainda infértil. No terceiro mês, o casal original gera mais um casal e o segundo casal fica fértil. Portanto, nesse terceiro mês teremos três casais. Agora, os dois primeiros casais estão férteis e geram, cada um, um novo casal. Dessa forma, o número de casais no quarto mês será 5. E assim por diante.
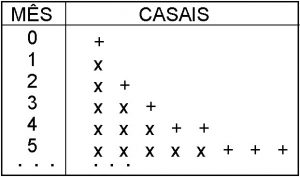
O resultado é uma seqüência de números em que cada um deles é obtido pela soma dos dois números imediatamente anteriores:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
Esta é a “seqüência de Fibonacci”.
A expressão que dá o número de Fibonacci de ordem n é, simplesmente:
F ( n ) = F ( n – 1 ) + F ( n – 2 ).
Pulando mais alguns séculos chegamos a Johannes Kepler, o célebre astrônomo das três leis. Kepler notou, em 1611, que a divisão entre um número de Fibonacci e seu precedente leva ao número Ф quando se avança para valores cada vez maiores na seqüência. Em termos matemáticos, isto quer dizer que F(n) / F(n – 1) tende para Ф quando n tende para infinito. Pegue uma calculadora e verifique isso.
De modo inverso, os números de Fibonacci podem ser gerados a partir de potências de Ф segundo a expressão:
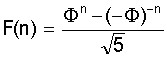
O interessante nessa expressão é que os números da série de Fibonacci, que são racionais, podem ser gerados de potências de Ф, que é irracional. Tecnicamente, diz-se que os números de Fibonacci seguem uma “lei de potência”. Números com essa propriedade não são completamente aleatórios.
Outra forma de escrever o termo de ordem n da série de Fibonacci, que convido vocês a demonstrarem, está indicada na expressão abaixo. Ela ilustra, mais uma vez, a relação entre os números de Fibonacci e a razão áurea.
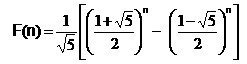
A seguir, vou mostrar para vocês algumas propriedades curiosas do número Ф.
Algumas propriedades numéricas do número Ф.
O número Ф, por si mesmo, já tem algumas propriedades curiosas. Como vimos, ele é irracional, como seu colega mais famoso, o número . Isto significa que esses números não podem ser obtidos pela divisão de dois inteiros. Só que, no meu modo de ver, o número Ф é mais sofisticado e imprevisível. Ele pode surgir de expressões matemáticas bastante curiosas. Por exemplo, considere a expressão abaixo:
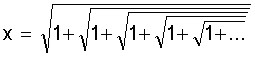
Parece muito complicado, mas, na verdade, é bem fácil mostrar que esse número x é justamente nosso Ф. Tome o quadrado de ambos os lados dessa expressão:
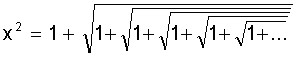
Ora, como o número de raízes é infinito, o segundo termo do lado direito da equação acima é justamente x. Logo, temos:
x² = 1 + x.
Portanto, como vimos anteriormente, resulta que x = Ф.
Outra expressão curiosa que leva a Ф é essa:
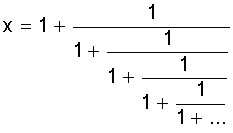
Deixo a vocês a tarefa simples de mostrar que esse x também é nosso querido Ф. Mas, quero aproveitar essa fração que não acaba nunca para comentar que o número Ф talvez seja o mais irracional dos números irracionais. Pois essa fração converge tão vagarosamente para ф que parece nos mostrar a relutância de Ф em se associar a uma fração, mesmo que a fração não seja de inteiros.
O quadrado de Ф, isto é, ФФ, vale 2,6180339887 …
Como vemos, o número ФФ é o próprio número Ф acrescido de 1. Além disso, o inverso de Ф, isto é, 1 / Ф é igual a 0,6180339887 …, que é Ф-1 e, como vemos, é o outro ф, definido anteriormente. Portanto, o número Фф é igual a 1.
Podemos construir uma seqüência que chamarei de “seqüência de Fifibonacci”, formada pelos quadrados dos números de Fibonacci. Ela é:
1, 1, 4, 9, 25, 64, 169, 441, 1156, 3025, 7921, …
É claro que a fração entre dois números consecutivos dessa seqüência converge para o número ФФ = 2,6180339887 … Deixo para vocês a tarefa de encontrar uma regra de formação para essa seqüência.
Além dessas propriedades numéricas o número Ф também tem algumas curiosas propriedades geométricas, como veremos a seguir.
Propriedades geométricas do número Ф.
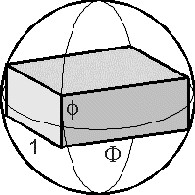
O tijolo de Fibonacci é um paralelepípedo de lados 1, Ф e ф. Ele tem volume unitário e a área total de suas faces é 4Ф . Esse tijolo pode ser inscrito em uma esfera de raio 1. Portanto, a razão entre as áreas da esfera e do tijolo inscrito é / Ф, curioso encontro entre dois prestigiosos números irracionais.
Podemos, também, construir o tijolo de Fifibonacci, com lados 1, ФФ e фф. Esse tijolo também tem volume unitário mas sua área total é igual a 8, um saudável retorno à racionalidade.
A letra Ф é a 21ª letra do alfabeto grego. 21, é claro, é um dos números de Fibonacci. Os esotéricos adoram essas coincidências e ficam imaginando códigos secretos relacionados com esses números. Meu nome, por sinal, tem 5 e 8 letras, dois números consecutivos na seqüência de Fibonacci, o que, presumivelmente, me confere poderes mágicos, mesmo sem ter de gritar Shazam.
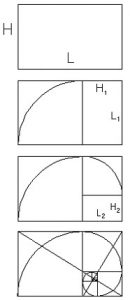
A origem de Ф, como vimos, foi geométrica. A proporção áurea foi muito utilizada por artistas da pós-renascença na composição de seus quadros. Uma construção geométrica que leva a um resultado interessante começa com um retângulo onde a razão entre a largura L e a altura H seja justamente Ф. Esse é um retângulo áureo. Rebatendo um lado de altura H, obtemos um quadrado e outro retângulo áureo, este de lados L1 e H1. Pois L1 / H1 = Ф, novamente.
Se o processo for repetido no segundo retângulo áureo, obtemos outro quadrado e outro retângulo, também áureo, sendo L2 / H2 = Ф. E aí você toma gosto e vai repetindo a brincadeira até enjoar, obtendo retângulos áureos cada vez menores que convergem para um ponto que chamamos de pólo da construção. É fácil ver que esse pólo é o encontro de todas as diagonais maiores de todos os retângulos áureos da construção.
Os matemáticos adoram dar nomes grandiosos a seus objetos. O próprio nome da proporção áurea já é desse tipo. Pois esse pólo é chamado, por eles, de “olho de Deus”. Descontando a pretensão, vale a pena mencionar que a curva que leva ao pólo aproxima-se de uma espiral logarítmica que René Descartes chamava de “espiral equiangular”, pois traçando qualquer reta a partir do pólo ela corta a curva sempre com o mesmo ângulo. Então, esse pode ser o mote para que eu comece a mostrar a vocês como o número Ф e a seqüência de Fibonacci surgem em coisas da natureza.
O número Ф na natureza.
Dizem que as aves predadoras, como águias, falcões e gaviões, descem sobre suas presas seguindo uma espiral equiangular, com a presa no pólo. Como os olhos das aves são laterais, fazendo isso, a ave mantém a presa sempre na mesma linha de visão sem que precise girar a cabeça, o que prejudicaria a aerodinâmica do vôo.
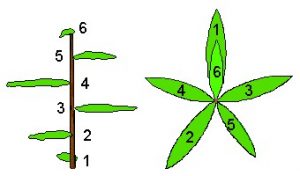
No mundo vegetal o número Ф e a seqüência de Fibonacci surgem em muitas situações. O arranjo dos galhos nos troncos das árvores e das folhas nos galhos costuma seguir uma seqüência de Fibonacci. Partindo de uma folha baixa, contamos o número de voltas em torno do galho até chegar a outra folha exatamente acima da inicial. Na figura, partindo da folha (1), precisamos de 3 rotações no sentido horário para chegarmos à folha (6) que está diretamente sobre a primeira. Nessas 3 voltas, passamos por 5 folhas. No sentido anti-horário, bastam 2 voltas. Note que 2, 3 e 5 são números de Fibonacci.
Correndo o risco de ser prematuramente classificada como caduca, comprovei essa tendência dos vegetais em vários exemplares de plantas, como esse singelo arbusto fotografado por meu neto Antônio no quintal de nosso sítio na Meruoca. Nesse caso, precisei de 5 voltas no sentido horário para encontrar um galho exatamente sobre o mais baixo, passando por 8 galhos no processo.
Os botânicos acham que essa forma de dispor folhas e galhos tem uma razão prática, aproveitada pela seleção natural. Ela torna mais eficiente a utilização da luz solar e a exposição às gotas da chuva. Faz sentido, mas a seqüência de Fibonacci e sua espiral característica também aparecem em situações vegetais onde a explicação não é tão evidente.
Um bom exemplo é o abacaxi, essa deliciosa fruta que, dizem as más linguas, é o símbolo de nosso cinema. Nessa fotografia de um belo abacaxi (Antônio, novamente), podemos ver as espirais formadas pelos gomos da casca. Cada gomo tem a forma aproximada de um hexágono e participa de três espirais que se cruzam. Formando o menor ângulo com o eixo do abacaxi, 8 espirais paralelas circulam a fruta. Com um ângulo maior, são 13 espirais paralelas e com ângulo maior ainda, são 21 espirais. Não preciso nem lembrar que 8, 13 e 21 são números sucessivos na seqüência de Fibonacci.
Coisa parecida, e até mais evidente, acontece com os girassóis, onde o número de espirais formadas pelas sementes da flor é bem grande. Infelizmente, não encontrei girassóis em nosso jardim para fotografar. Recomendo que procurem em outros jardins.
Até agora ainda não falei de situações físicas onde o número Ф e a série de Fibonacci aparecem. Pois, vou falar a seguir.
O número Ф e a série de Fibonacci na física.
Existem áreas da física onde os números de Fibonacci surgem por construção proposital e dão resultados interessantes. Veja, inicialmente, um exemplo muito simples. Temos duas placas de vidro, com índices de refração diferentes, justapostas uma sobre a outra. Um raio de luz que incida sobre esse conjunto pode sofrer reflexões e desvios. Vamos contar o número de caminhos possíveis de um raio de luz aumentando, gradualmente, o número de reflexões nesses caminhos.
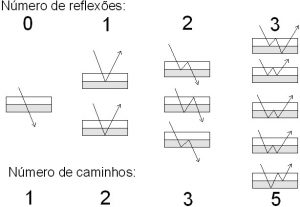
Olhando a figura, podemos ver que o número de caminhos segue a seqüência de Fibonacci. Representando o número de reflexões, chamado de “geração”, pela letra n, o número de caminhos será F(n), um número de Fibonacci. Por exemplo, a geração n = 4 leva a F(4) = 8 caminhos.
O físico nordestino Eudenilson Lins de Albuquerque é um especialista no estudo das propriedades físicas de camadas de materiais empilhadas segundo seqüências de Fibonacci. Dos trabalhos que ele já publicou pincei um exemplo relativamente simples.
Formam-se pilhas com camadas de dois materiais transparentes com índices de refração diferentes. A figura mostra como montar essas pilhas segundo um esquema tipo Fibonacci. Cada pilha é formada colocando-se as duas pilhas anteriores uma sob a outra.
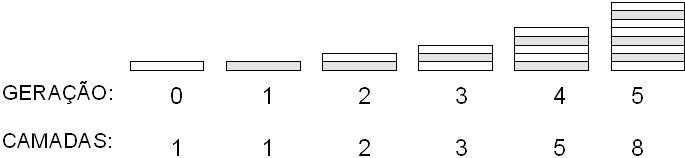
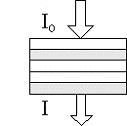
Um problema físico interessante consiste em saber quanta luz consegue atravessar uma dessas pilhas. Isto é, procura-se saber qual é a “transmitância” T da luz através da pilha, sendo T definido como T = I / I0, onde I0 é a intensidade da luz incidente e I é a intensidade da luz que sai do outro lado da pilha.
As espessuras das camadas são feitas de modo a serem “oticamente equivalentes”. Isto significa que a luz leva um tempo igual para atravessar qualquer um dos dois tipos de camada ou, o que é o mesmo, que o comprimento de onda da luz é igual em camadas de tipos diferentes. Com esse arranjo, surgem interessantes casos de interferência entre os feixes de luz que se refletem nas interfaces entre camadas vizinhas. Por exemplo, se a espessura ótica das camadas for exatamente igual a meio comprimento de onda da luz, isto é, d = λ / 2, os feixes refletidos nas faces sucessivas interferem destrutivamente e se aniquilam mutuamente. Nesse caso, portanto, a transmissão de luz pelas camadas é completa, T = 1. Se a espessura das camadas for igual a um quarto de um comprimento de onda da luz, isto é, d = λ / 4, os feixes refletidos se reforçam mutuamente e a transmissão é incompleta, T < 1. Para outros comprimentos de onda da luz, T varia entre esses dois valores extremos. Quando o número de camadas cresce segundo as gerações de Fibonacci, a transmissão de luz varia entre 0 e 1 de uma forma que depende da ordem na seqüência.
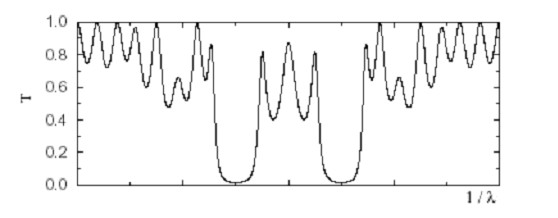
Essa figura, que foi adaptada de um dos trabalhos de Eudenilson, mostra como a transmissão de luz (T) varia com o comprimento de onda da luz incidente para uma pilha correspondente à geração S7, com 13 camadas. Um resultado interessante é que a forma dessas curvas de transmissão se reproduz a cada 6 gerações de Fibonacci. Isto é, essa figura também está mostrando T para uma pilha correspondente à geração S13, com 233 camadas. Basta ajustar a escala dos comprimentos de onda de forma adequada.
Sempre que surge uma reprodução de formas desse tipo diz-se que a curva estudada tem “propriedade de escala”. Os físicos adoram encontrar essas “leis de escala” em seus modelos e experimentos. Esse comportamento que acabamos de relatar, talvez seja mais uma manifestação da não-aleatoriedade dos números de Fibonacci, mencionada anteriormente.
Vamos agora falar do problema de preencher um plano com mosaicos de formas arbitrárias. É um problema geométrico com implicações na física dos sólidos, como veremos. Se os mosaicos tiverem a forma de polígonos regulares, com lados e ângulos iguais, topamos logo com uma limitação. Triângulos, quadrados e hexágonos regulares podem ser usados para cobrir um plano, mas, pentágonos não servem para isso. Quando tentamos cobrir um piso com mosaicos pentagonais logo constatamos que sobram espaços vazios. Essa observação levou os cristalógrafos à conclusão de que não poderiam existir cristais onde os átomos e moléculas se ajustassem formando uma simetria pentagonal, também chamada de “simetria de ordem-5”.
Mas, o plano pode ser preenchido com mosaicos não-regulares. Ou, com mais de um tipo de mosaico, com formas diferentes. O incrível pintor holandês Mauritius Escher, que uma vez me presenteou com uma de suas belas gravuras, era um mestre nessa arte de preencher planos com figuras de todo tipo. Sem a sofisticação dos quadros de Escher, podemos ver que um piso pode facilmente ser coberto, sem deixar vazios, por mosaicos hexagonais e pentagonais, em um padrão semelhante ao que vemos nas bolas de futebol.
Existe um tipo muito interessante de mosaico, inventado por um matemático inglês, que utiliza amplamente as propriedades do número Ф. É disso que falarei a seguir.
Roger Penrose, seus mosaicos e a consciência.
O físico inglês Roger Penrose, que foi orientador do famoso Stephen Hawking, inventou um tipo de mosaico de duas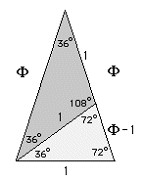 
formas com características aparentemente contraditórias: tem simetria de ordem-5, preenche o plano e não é periódico. Os mosaicos de Penrose são formados a partir de um triângulo isósceles de lados iguais a Ф. Esse triângulo converte-se em dois, mostrados com cores diferentes na figura, dividindo-se um dos lados em uma parte que mede 1 e outra que mede Ф – 1. Combinando esses novos triângulos, Penrose montou dois tipos de mosaico, uma seta e uma arraia (que os sulistas chamam de pipa). Usando esses dois “mosaicos de Penrose” o plano pode ser preenchido. Mais uma vez, não preciso nem dizer como esse mosaico está repleto de proporções áureas.
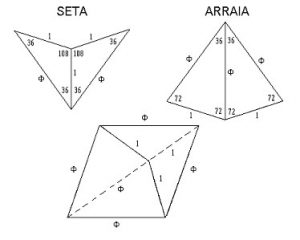
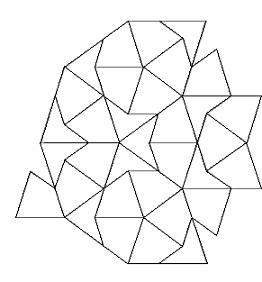
É surpreendente que, se dividimos o número de arraias pelo número de setas em uma dada área do mosaico de Penrose, essa fração tende para Ф quando a área examinada é cada vez maior.
Os mosaicos de Penrose cobrem uma superfície plana bi-dimensional, mas, os matemáticos já acharam pares de formas volumétricas que preenchem por completo o espaço tri-dimensional. São objetos que lembram cubos com faces repuxadas, todas idênticas aos mosaicos planos de Penrose. São chamados, por causa disso, de “romboedros áureos”.
O que não se esperava, porém, é que a simetria de ordem-5, presente nos mosaicos de Penrose e nesses romboedros que enchem o espaço, pudesse surgir em objetos físicos reais, como sólidos. Mas, surgiu. Na década de 80 do século passado foram descobertos certos materiais que tinham simetria de ordem-5 e um arranjo não-periódico. Foram chamados de “quase-cristais”, pois têm simetria de rotação, como os cristais normais, mas, não têm simetria de translação, isto é, não possuem uma “célula” que se repete periodicamente em alguma direção espacial.
Penrose, que é um especialista em buracos-negros, inventou seus mosaicos meio de brincadeira e não esperava que eles chegassem a ser úteis na descoberta e explicação dos quase-cristais. Mais recentemente, Penrose passou a se dedicar à tarefa de procurar explicações para a consciência, essa propriedade espantosa que temos de pensar, fazer associações e buscar explicações até para a própria consciência, em um processo auto-recorrente um tanto vertiginoso. Penrose acha que a consciência pode ser o resultado de processos quânticos que têm lugar no interior dos microtubos, um emaranhado de filamentos que formam o citoesqueleto, estrutura presente em todas as células dos seres vivos. Segundo Penrose, os microtubos seriam o local mais propício para abrigar os processos quânticos que resultariam na consciência. Não creio que valha a pena entrar nos detalhes desse palpite de Roger Penrose mas cabe contar como ele envolve também os números de Fibonacci.
A parede de um microtubo é formada por colunas de unidades chamadas de “tubulins”. Ao todo, um microtubo tem 13 colunas de tubulins. A disposição dos tubulins forma espirais que lembram as espirais desenhadas pelos gomos do abacaxi. Como vemos no desenho, seguindo as espirais em torno do microtubo, encontramos padrões que se repetem a cada 3, 5, 8 e 13 unidades. Todos esses números, é claro, fazem parte da seqüência de Fibonacci.
Tem gente que já sugeriu que o aparecimento dos números de Fibonacci nos microtubos não se dá por acaso. Do mesmo modo que o arranjo de Fibonacci facilita o aproveitamento da luz do sol e da água da chuva nas folhas e nos galhos das árvores, também poderia promover o fluxo de informações nos microtubos. Haja especulação, mas, pelo menos, é uma especulação excitante.
Muito mais há para contar sobre esses maravilhosos números mas acho melhor parar por aqui. Com essa introdução vocês já estão prontos para adquirir a mania de encontrar a proporção áurea e os números de Fibonacci nas coisas do mundo em que vivem. Quem sabe, até descobrir novas associações ainda desconhecidas. Além disso, existem outros números interessantes, além do número Ф, que são objeto de vários textos nesse mesmo local. Sugiro que vocês leiam sobre eles.
