O Movimento Browniano
Esse curioso movimento, observado por Robert Brown em 1827, serviu de teste definitivo para comprovar a existência de átomos e moléculas.
Em 1827, o botânico escocês Robert Brown observou e descreveu esse tipo de movimento irregular executado por pequenos grãos de pólen de flores suspensos em água. Foi uma observação singela e aparentemente trivial mas, com o desenrolar dos acontecimentos, revelou-se de extrema importância, resolvendo uma longa disputa sobre a existência de átomos e moléculas. A partir do relato de Brown, vários trabalhos foram apresentados sobre esse curioso movimento, culminando com um artigo publicado, em 1905, pelo então desconhecido Albert Einstein.
Hoje em dia, o “movimento browniano” serve de modelo na descrição de flutuações que ocorrem nos mais diversos e inesperados tipos de sistemas. Por exemplo, praticamente a mesma descrição e o mesmo tratamento matemático de Einstein podem ser adaptados para descrever flutuações de preços de mercadorias, a condutividade elétrica em metais e a ocorrência de cheias nos rios.
Nos capítulos seguintes, tentaremos dar uma idéia do que é o movimento browniano e contar como seu estudo deu origem a todo esse rico e complexo campo de pesquisas.
Capítulo 1: Os átomos e as moléculas existem?
Essa pergunta pode soar estranha aos seus ouvidos modernos, mas, na segunda metade do século 19, era motivo de debates na comunidade de físicos e químicos. O estudo dos gases dava suporte aos que acreditavam na existência dessas entidades tão pequenas que ninguém conseguia ver nem medir, mas, isso não bastava para alguns cientistas da época.
Ernst Mach
Ludwig Boltzmann
O físico austríaco Ludwig Boltzmann, que viveu nesse tempo, desenvolveu sua física estatística em torno das propriedades das hipotéticas moléculas. Outros cientistas, porém, preferiam acreditar que a matéria é contínua e achavam que era possível descrever todos os fenômenos naturais sem precisar dessas minúsculas partículas. Os mais influentes entre esses eram o químico Wilhelm Ostwald e o físico e filósofo Ernst Mach.
Não pense que a disputa entre esses cidadãos era só de alto nível, puramente científica. Os argumentos eram tão acalorados que Boltzmann, angustiado pela violenta rejeição a suas teorias moleculares, tentou o suicídio por duas vezes, morrendo na segunda.
Que argumentos eram usados contra a hipótese atômica? O mais comum se baseava no sucesso do cálculo infinitesimal na explicação dos fenômenos naturais. Um mundo feito de átomos, segundo esses argumentos, sendo discreto e descontínuo, não funcionaria como previsto pelas equações diferenciais. Outra objeção era baseada na reversibilidade dos processos moleculares. Como o mundo que conhecemos é naturalmente irreversível, Ostwald e Mach apontavam essa discrepância como indicativa da não existência de átomos.
O grande filósofo Leibnitz tinha um argumento fortíssimo para demonstrar que os átomos não existem. Ele desafiava a alguém encontrar duas folhas de grama exatamente iguais uma a outra. Ou duas gotas de leite idênticas, vistas no microscópio. Se os átomos existissem, dizia Leibnitz, como uma folha teria um número finito de átomos, deveria ser possível e fácil achar duas folhas exatamente iguais. Como ninguém acha, por mais que procure, os átomos não devem existir.
Mais adiante, veremos qual é o furo nesse argumento de Leibnitz. Como não podia deixar de ser, quem acabou resolvendo essa disputa foi a experiência. No fim, a própria natureza indicou o lado certo. E tudo se originou em uma singela observação de um botânico inglês chamado Robert Brown. Nos capítulos seguintes, veremos o que Brown descobriu e como sua descoberta foi interpretada.
Capítulo 2: O enigmático movimento observado por Robert Brown.
Microscópio de Robert Brown.
Em 1928, foi publicado, na revista científica inglesa Philosophical Magazine, um artigo com o simpático título “Uma breve descrição de observações microscópicas efetuadas nos meses de Junho, Julho e Agosto de 1827 sobre partículas contidas no pólen de plantas”. Seu autor, o botânico Robert Brown, observou, através do microscópio visto ao lado, pequenos grãos de pólen de plantas, tão leves que flutuavam dentro de água. O que ele achou surpreendente e inexplicável foi o movimento incessante desses grãos, deslocando-se de um lado para o outro em uma dança de São Guido interminável. Inicialmente, Brown pensou que esse movimento fosse causado por algum minúsculo ser vivo morando dentro do grão. Mas, não demorou para que ele observasse o mesmo tipo de comportamento em partículas de cinza e poeira flutuando em água. Finalmente, essa explicação biológica foi descartada por uma razão definitiva. Brown encontrou uma amostra de quartzo que tinha bolhas internas contendo água onde flutuavam pequenas partículas de poeira, exibindo o mesmo movimento desordenado dos grãos de pólen. Como era evidente que essas partículas estavam encerradas nas bolhas do quartzo por milhões de anos, não poderia haver nada vivo dentro delas.
A partir da publicação do artigo de Brown, muitos palpites foram dados para explicar esse fenômeno que ficou conhecido como “movimento browniano”. Talvez as partículas se movessem por causa de variações locais de temperatura do líquido, ocasionando correntes de convecção. Se isso fosse verdade, duas partículas bem próximas uma da outra deveriam se mover na mesma direção. E isso simplesmente não ocorria. E assim, uma após a outra, várias “explicações” foram descartadas. Até que surgiu a idéia de associar esse movimento ao movimento das moléculas da água. Ninguém via as moléculas de água (se é que elas existiam mesmo), mas, alguns caras mais espertos começaram a acreditar que elas não só existiam como causavam o movimento browniano. Em 1877, o jesuita belga Joseph Delsaulx escreveu: “No meu modo de pensar, esse fenômeno se deve ao movimento térmico das moléculas do líquido que circunda as partículas”. Na mosca!
Só que, em ciência, não basta dar palpites. Tem de explicar direitinho, de preferência com cálculos, fórmulas e, o que é mais interessante, previsões de outros resultados. Quem fez esse trabalho foi o jovem (na época) Albert Einstein. Vamos falar sobre isso mais adiante, mas, preparando o terreno, vamos descrever, no próximo capítulo, uma visão microscópica das origens do movimento browniano.
Capítulo 3: Uma explicação preliminar para o movimento browniano.
Descartada a hipótese de que os grãos de pólen seriam empurrados por seres vivos microscópicos, e depois que Brown mostrou que também não eram movidos por correntes no líquido, restou a questão: quem está empurrando esses grãos de um lado para o outro?
O próprio Brown já achou as primeiras pistas para a correta explicação do movimento que observara. Em seu artigo, ele já informava que o movimento das partículas menores era mais rápido e vigoroso que o movimento das mais pesadas. Além disso, se o líquido fosse mais viscoso, o movimento ficava mais lerdo.
Com essas e outras observações, surgiu a idéia de explicar o movimento dos grãos como o resultado de minúsculos empurrões dados pelas moléculas do líquido. Essas moléculas seriam pequenas demais para serem vistas, mesmo em um microscópio, mas estariam em perpétuo movimento e se chocariam, continuamente, com a superfície do grão. Normalmente, como o movimento das moléculas seria totalmente desordenado, o grão receberia empurrões por todos os lados e ficaria parado. Mas, ocasionalmente, era provável que mais moléculas empurrassem em um sentido que no sentido oposto. Sempre que isso ocorresse, e o saldo de empurrões para um determinado lado fosse positivo, o grão se deslocaria para esse lado.
No próximo capítulo, daremos uma idéia dos números envolvidos. Vamos ver qual é o tamanho médio das moléculas e quantas existem em uma gota de líquido. Esses valores são fundamentais para entender o comportamento dessas minúsculas entidades.
Capítulo 4: O número de Avogadro. O engano de Leibnitz.
Quantas moléculas de ar (gás), ou de água (líquido), cabem em um centímetro cúbico? No tempo de Robert Brown, e até o final do século 19, ninguém sabia responder essa pergunta. Assim mesmo, em 1811, o italiano Amedeo Avogadro fez uma afirmativa audaciosa. Ele disse: “Não sei quantas moléculas de um gás existem em um centímetro cúbico. Mas, afirmo que o número delas é sempre o mesmo, qualquer que seja o gás”.
É claro que Avogadro não usou exatamente essas palavras mas a idéia foi essa mesma. Não vamos contar aqui a história dessa idéia de Avogadro – faremos isso em outra ocasião. Basta, para entendermos o movimento browniano, saber quanto vale o “número de Avogadro”. Esse número diz quantas moléculas de um gás (qualquer gás) existem em um volume de 22,4 litros em condições normais de temperatura e pressão. A escolha desse volume é arbitrária – qualquer outro serviria – mas está ligada a outros fatos que não relataremos aqui. Pois bem, o número de Avogadro vale:
N0 = 60229000000000000000000 moléculas.
Com números grandes assim, é melhor usar a notação científica:
10 = 101, 100 = 102, 1000 = 103 etc.
Logo, N0 = 6,0229 x 1023 moléculas.
Esse número é gigantesco. A gente de vez em quando vê algum autor tentando dar uma idéia da enormidade do número de Avogadro. Por exemplo, se a gente pudesse empilhar o número de Avogadro de folhas de papel A4, que altura teria a pilha? Faça as contas: uma folha de papel tem 0,05 milímetros de espessura. A distância da Terra ao Sol são 150 x 106 quilômetros. Será fácil calcular que a pilha seria 200 milhões de vezes mais comprida que a distância da Terra ao Sol.
Isso mostra como as moléculas e átomos são pequenos. E mostra porque o argumento de Leibnitz estava completamente furado. Sendo o número de átomos em uma folha da ordem de grandeza do número de Avogadro, o número de maneiras de formar uma folha é tão grande que não é nenhuma surpresa que a gente nunca encontre duas folhas iguais.
Até o início do século 20 ninguém ainda conseguira medir, de alguma forma, o número de Avogadro. Mas, logo nos primeiros anos desse século, várias sugestões foram apresentadas com métodos de fazer essa medida. Planck deu uma delas e Einstein, então com 25 anos, deu outra, utilizando – sabe o que? – o movimento browniano. Esse será nosso assunto nos próximos capítulos.
Capítulo 5: A tese de doutoramento do jovem Albert Einstein
Não vamos dar detalhes da tese de doutoramento que Albert Einstein apresentou à Universidade de Zurich, em 1905. Estamos apenas querendo mostrar que até os grandes gênios cometem erros inexplicáveis, ao mesmo tempo que produzem maravilhas.
Em sua tese, Einstein descreveu o comportamento de uma solução diluída – água com açucar, por exemplo. Com argumentos de hidrodinâmica, ele achou uma expressão matemática para o coeficiente de difusão das moléculas de açúcar na água. No próximo capítulo, veremos melhor o que é esse coeficiente. Por enquanto, basta saber que, usando o coeficiente de difusão e a viscosidade da água, Einstein obteve um valor para o número de Avogadro:
N0 = 2,1 x 1023 moléculas.
Esse número é cerca de três vezes menor que o correto, como sabemos hoje. A diferença, como foi verificado depois, decorreu de um erro no cálculo da viscosidade da solução. A fórmula que Einstein deduzira para essa viscosidade estava errada! Alguns anos mais tarde, Jean Baptiste Perrin mediu, no laboratório, a viscosidade da solução e detetou o erro no valor usado por Einstein. Informado disso, Einstein refez seus cálculos e encontrou o erro de matemática que cometera. Rapidamente, achou uma nova fórmula para a viscosidade e recalculou o número de Avogadro, dessa vez achando o valor correto.
Como você vê, até Einstein fazia contas erradas. Mas, não use essa desculpa para justificar seus erros nos trabalhos de casa.
Capítulo 6: Uma lista de coisas que precisamos conhecer.
Preparando o terreno para o que veremos nos próximos capítulos, vamos apresentar alguns conceitos físicos que serão usados a seguir. São eles: 1) caminhada aleatória; 2) difusão; 3) livre caminho médio. Supomos que você tem uma idéia do que é a viscosidade de um líquido. Se sabe que o óleo lubrificante é mais viscoso que a água, é suficiente.
Caminhada aleatória.
Essa é fácil de entender. Imagine um cidadão que sai do bar muito para lá de Marrakesh. A cada passo, ele muda a direção de sua trajetória, totalmente ao acaso. Ele percorre, nesse caso, uma “caminhada aleatória”, com uma forma parecida com a que vemos na figura (1). É fácil simular uma caminhada dessas, no papel ou no computador. Os passos devem ser, aproximadamente, do mesmo tamanho e o ângulo entre as direções de dois passos sucessivos é escolhido aleatoriamente entre 0 e 360 graus.
A figura (2) mostra (com alguma liberdade poética) uma caminhada dessas, depois de 100 passos. O caminhante andou um bocado mas, na verdade, se afastou pouco do ponto inicial. O círculo verde mostra, mais ou menos, de quanto o caminhante se afastou do ponto inicial. No entanto, é fácil ver que, depois de tanto andar, ele praticamente continua no ponto inicial. A região do ponto inicial continua sendo a mais visitada pelo caminhante em sua viagem desvairada. A figura (3) mostra a situação depois de 300 passos. Embora o caminhante já tenha alcançado pontos mais distantes do centro (círculo azul), a região central continua sendo o local mais provável de encontrá-lo. Essa é uma característica da caminhada aleatória: a região inicial permanece a mais visitada pelo caminhante, mesmo depois de um número enorme de passos. Fica fácil de entender quando dizemos que, depois de muito andar, o caminhante aleatório não saiu do canto.
Pode ser mostrado que o avanço médio da partícula depende do número de passos da seguinte forma. Mede-se o raio R do círculo até onde a partícula avançou. Na figura (2) seria o raio do círculo verde, na figura (3) seria o raio do círculo azul. Toma-se o quadrado desse raio. Esse valor depende do número de passos. Isto é, R2médio = L x N, onde L é o comprimento de cada passo e N é o número de passos.
Difusão.
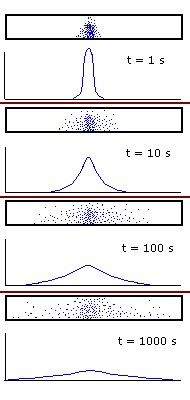Todo mundo tem uma idéia do que significa “difusão”, mas, vamos dar uma definição um pouco mais técnica. Imagine que alguém pinga uma gota de perfume no meio de um longo corredor, com 20 metros de comprimento. A figura tenta mostrar o que acontece com as moléculas do perfume. A partir do instante inicial, quando se concentram no ponto onde caiu a gota, elas se difundem pelo corredor. A densidade de moléculas de perfume inicialmente só é diferente de zero no ponto onde caiu a gota e elas sempre se difundem dos pontos onde a densidade é maior para pontos onde ela é menor. As curvas mostram os valores da densidade em vários instantes. Observe que, a medida que as moléculas se difundem pelo corredor, a densidade no ponto central vai diminuindo. No entanto, em todos os instantes, ela será sempre maior no centro. Os tempos ilustrados na figura são apenas para dar uma idéia da velocidade de propagação. E é aí que reside um dos erros de interpretação da difusão.
O tratamento matemático da difusão tem sutilezas. Para saber como a partícula avança a medida que o tempo passa poderíamos pensar em definir uma velocidade de avanço como sendo o raio do círculo R dividido pelo tempo. Essa definição não serve, porém. O correto é definir um coeficiente de difusão D como sendo a divisão do quadrado do raio pelo tempo. Isto é, D = R2/ t.
Livre caminho médio
Se uma gota de perfume cair no meio de um corredor de 20 metros de comprimento, alguém que esteja em um dos extremos do corredor sentirá o cheiro quase imediatamente. Mas, a julgar pela figura acima, o cheiro levaria uns 20 segundos para chegar ao fim do corredor. Para explicar o que realmente acontece, precisamos entender como as moléculas de perfume se difundem pelo ar.
Uma molécula de perfume, saindo da gota no meio do corredor, vai receber empurrões das moléculas de ar, da mesma maneira que o grão de pólen de Brown é empurrado pelas moléculas de água. Só que uma molécula de perfume é muito mais leve que um grão de pólen. Um choque com uma molécula de ar impulsiona a molécula de perfume com alta velocidade, em uma direção aleatória. Essa velocidade vale, tipicamente, algo em torno de 250 metros por segundo. Se ninguém a impedisse, a molécula de perfume alcançaria o fim do corredor em apenas 0,04 segundos. Mas, dificilmente a molécula conseguirá vencer esses 10 metros sem antes se chocar com outra molécula de ar e ser projetada em uma direção bem diferente. O que vai acontecer é o seguinte: cada molécula anda apenas uma pequena distância entre dois choques sucessivos com moléculas de ar. E aí, utilizamos o truque de achar um valor médio. Se pudéssemos medir a distância percorrida por cada molécula, entre dois choques, poderíamos achar o valor médio dessa distância. Bastaria somar todas as distâncias medidas e dividir essa soma pelo número de moléculas de perfume que estão se difundindo. O valor obtido dessa forma chama-se de “livre caminho médio”, nome bem apropriado.
Mas, média é média. A partir do instante em que a gota caiu, algumas moléculas que se soltaram dela só vão conseguir percorrer uma fração de milímetro antes de se chocar com uma molécula de ar. Outras, porém, vão conseguir percorrer distâncias bem maiores, até de metros, sem encontrar uma molécula de ar. Essas sortudas são muito poucas, mas, são elas que chegarão em pouco tempo ao nariz do cara que está no fim do corredor.
Capítulo 7: O artigo de Einstein sobre o movimento browniano.
A explicação completa e rigorosa do movimento browniano foi dada pelo jovem e até então desconhecido Albert Einstein, no chamado “ano milagroso” de 1905. Nesse ano, Einstein publicou uns poucos artigos que abalaram a Física. Um deles se intitulava “Sobre o movimento de partículas suspensas em um fluido em repouso”.
Não vamos dar detalhes sobre esse trabalho de Einstein mas vale a pena conhecer seus principais resultados. O principal interesse de Einstein era achar uma expressão para o movimento das moléculas do fluido que servisse para calcular o número de Avogadro. Aparentemente, ele nem conhecia direito o trabalho de Brown. Considerando os fatores que influenciam o movimento das moléculas, tais como a temperatura e a viscosidade do fluido, conseguiu demonstrar uma fórmula para o coeficiente de difusão. Essa fórmula envolvia o número de Avogadro. Portanto, seria possível, para um experimental que medisse a difusão das partículas em suspensão, obter o valor desse número.
A expressão determinada por Einstein foi: D = (RT/N)(1/6 πr)
onde R é a constante dos gases, T é a temperatura, N é o número de Avogadro, π é a viscosidade do fluido e r é o raio da molécula. Medindo D e sabendo os outros valores, calcula-se N.
Pelos resultados obtidos por Einstein, quanto menores fossem as moléculas do fluido, menor seria o movimento das partículas em suspensão. Isto é, se o fluido não fosse feito de moléculas, se fosse completamente contínuo, infinitamente divisível, as partículas brownianas não se moveriam! Portanto, a própria observação de que elas se movem é uma evidência irrefutável da existência das moléculas.
Na verdade, em seu artigo Einstein já usou o valor do número de Avogadro, medido por outras técnicas, para calcular que uma partícula em suspensão na água (viscosidade 0,0135) deveria avançar, em média, 0,006 milímetros em um minuto. Essa previsão foi completamente comprovada pelas medidas de Perrin, como veremos mais adiante.
Capítulo 8: Uma trajetória cheia de truques.
O caminho que uma partícula browniana percorre é irregular e imprevisível. Não dá para descrever rigorosamente essa trajetória, nem com palavras nem com uma expressão matemática. Aliás, os matemáticos sofrem um bocado com esse tipo de “curva”, toda feita de ângulos e desvios súbitos. Tecnicamente, eles dizem que essa curva é “patológica”, é uma curva contínua mas não tem derivada contínua em nenhum de seus pontos.
Alguns anos depois do trabalho de Einstein, o matemático Nobert Wiener provou que a trajetória browniana tem comprimento infinito entre dois pontos quaisquer. O caminho traçado pela partícula é tão enrolado que, se esperássemos um tempo infitamente longo, ela percorreria todo o plano, sem deixar de passar por nenhum ponto. Tecnicamente se diz que, contrariando as aparências, o caminho percorrido pela partícula browniana não é uma linha (com dimensão 1), mas é uma superfície (com dimensão 2)!
E tem mais: Não pense que a trajetória da partícula browniana parece ser irregular porque o microscópio não tem um aumento suficiente para mostrar os detalhes da curva. Nada disso. Com um microscópio mais potente veríamos mais detalhes, realmente, mas a curva seria tão angulosa e irregular quanto antes. Veja, na figura, como veríamos a curva usando microscópios cada vez mais poderosos.
Como vemos, o visual da curva percorrida pela partícula browniana é o mesmo, para qualquer aumento. Os cientistas dizem que uma curva com esse comportamento é “auto-similar”. Isto é, em qualquer aumento (ou “escala”) a curva parece sempre do mesmo jeitão.
É claro que isso tem um limite, no caso real, pois, se tivéssemos microscópios muito potentes acabaríamos vendo até as moléculas. Matematicamente, porém, não há limite para as escalas.
Hoje em dia, uma curva com esse tipo de propriedade é chamada de “fractal”. Esse é um interessante assunto, cheio de resultados curiosos, que abordaremos qualquer dia desses.
Capítulo 9: As experiências de Perrin e a vitória da hipótese atômica.
Em 1903 foi inventado um novo tipo de microscópio, o ultramicroscópio, bem mais poderoso que os outros microscópios em uso na época. Logo após a publicação do trabalho de Einstein, o francês Jean-Baptiste Perrin, que dispunha de um desses aparelhos, iniciou um projeto de verificar a validade e precisão das expressões deduzidas pelo jovem cientista.
O resultado dessas medidas foi uma comprovação cabal de todas as previsões de Einstein. Perrin conseguiu obter valores para o tamanho das moléculas do líquido e para o coeficiente de difusão das partículas suspensas. Essas medidas se ajustaram como uma luva às fórmulas sugeridas por Einstein. O número de Avogadro também foi obtido com uma excelente precisão. Com esses resultados, ficou definitivamente comprovada a existência de moléculas e átomos. E, por esses trabalhos, Jean-Baptiste Perrin foi agraciado com o prêmio Nobel de Física de 1926.
Uma curiosidade: outro francês, Louis Bachelier, em sua tese de doutoramento apresentada em 1900, cinco anos antes do artigo de Einstein, desenvolveu praticamente toda a teoria do movimento aleatório, obtendo expressões semelhantes às que seriam depois obtidas por Einstein. No entanto, Bachelier não descrevia um sistema físico, como partículas suspensas em água, mas as flutuações das ações de uma bolsa de valores. Por essa razão, seus resultados passaram inteiramente despercebidos pelos físicos da época. Hoje, sabe-se que o tratamento teórico dessas flutuações serve para explicar inúmeros fenômenos que ocorrem em áreas completamente distintas, como a física, a biologia, a economia e as ciências políticas. A observação aparentemente inocente de Robert Brown revelou-se muito mais importante do que parecia quando foi relatada pela primeira vez.
