Simetria
O conceito e as propriedades de SIMETRIA são intensamente usados pela Física, a Química e a Biologia. Veja como.
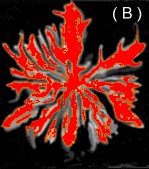
O objeto da figura (A) é simétrico. O objeto da figura (B) não é. Para qualquer um de nós, essa afirmação é tão evidente quanto dizer que (A) é azul e (B) é vermelho. Como distinguir um objeto simétrico de outro, não simétrico? A ciência tem métodos para isso. Um deles consiste em catalogar algumas operações ditas “de simetria” e testar como o objeto se comporta quando submetido a essas operações. Se, após a operação, o objeto estiver em uma configuração indistinguível da que tinha antes, diz-se que ele é simétrico em relação a essa operação. Explicaremos isso melhor nas próximas seções.
Entretanto, o estudo da simetria na Física, na Matemática e em outras ciências, envolve sutilezas bem mais profundas que um simples catálogo de operações. Nas seções que se seguem falaremos um pouco sobre essas utilidades técnicas da simetria. Depois de lê-las, talvez você passe a ver as simetrias desse mundo com outros olhos, descobrindo detalhes e conexões que antes passavam despercebidas.

Qual é termo seguinte da série acima?
NOTA: Um exemplo simples do uso da simetria na solução de um problema de Física é dado em nossa seção EIS A QUESTÃO.
Algumas operações de simetria.
 Você olha essa estrela e fecha os olhos. Enquanto está de olhos fechados, alguém gira a estrela de um ângulo de 72°. Quando você abre novamente os olhos não sabe dizer se a estrela foi movida ou não. Isso acontece porque fizeram sobre ela uma “operação de simetria”.
Você olha essa estrela e fecha os olhos. Enquanto está de olhos fechados, alguém gira a estrela de um ângulo de 72°. Quando você abre novamente os olhos não sabe dizer se a estrela foi movida ou não. Isso acontece porque fizeram sobre ela uma “operação de simetria”.
No caso, essa operação foi uma rotação em torno de um eixo que passa pelo centro geométrico da estrela (aquele ponto vermelho) e é perpendicular à tela de seu monitor.
72° é o ângulo entre duas pontas da estrela. O mesmo resultado ocorre se a estrela for girada de 144° (2 x 72°), de 216° (3 x 72°), de 288° (4 x 72°), ou, finalmente, de 360° (5 x 72°). Já que depois de 5 rotações a estrela fica exatamente como começou, diz-se que a rotação foi de ordem 5
OPERAÇÃO IDENTIDADE
Girar de 360° é o mesmo que girar de 0°, ou, simplesmente, nem girar. Pode parecer preciosismo técnico, mas, essa operação é tão importante que merece um nome especial: chama-se OPERAÇÃO IDENTIDADE.
OPERAÇÕES DE ROTAÇÃO
A operação que vimos acima, agindo sobre a estrela, é uma operação de rotação. No caso, tratava-se de uma operação de rotação de ordem 5. Uma operação de rotação implica na existência de um elemento de simetria, o eixo de rotação. No exemplo da estrela, esse eixo de rotação era perpendicular ao plano da estrela, passando por seu centro geométrico.

A estrela tem mais cinco eixos de rotação. A figura ao lado mostra um deles. Nesse caso, o eixo é de ordem 2. As rotações, portanto são de 180°. A cada duas rotações de ordem 2 a estrela volta à configuração original. O eixo de rotação pertence ao plano da estrela e passa pela bissetriz de uma de suas pontas. Os outros 4 eixos correspondem às outras 4 pontas.
Agora diga: quantos eixos de rotação você vê na figura abaixo?

Resposta: 1 eixo de rotação de ordem 6, perpendicular ao plano da figura e passando por seu centro; e 6 eixos de rotação de ordem 2. Se você esperar um pouco os 6 eixos de ordem 2 aparecem rapidamente.
OPERAÇÃO DE REFLEXÃO
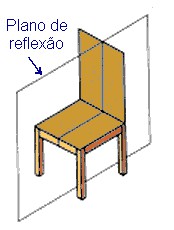
Observe o familiar objeto da figura ao lado. Ele não tem simetria de rotação. Por mais que você procure, não achará nenhum eixo de rotação. Entretanto, ele tem simetria de reflexão. Um espelho plano, se pudesse ser colocado na posição do plano visto na figura, geraria uma imagem que reproduz o objeto todo. O elemento de simetria, nesse caso, é um plano de reflexão.
É muito comum encontrar objetos que possuem simetria de rotação e reflexão, ao mesmo tempo. Tente localizar eixos de rotação (de qualquer ordem) e planos de reflexão nos objetos abaixo. Físicos do estado sólido e cristalógrafos fazem isso com tudo que passa por seus olhos. Acaba virando mania.

Operação de inversão
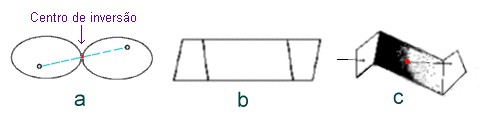
Essa operação de simetria, a inversão, tem como elemento de simetria um ponto chamado centro de inversão. Para qualquer ponto de um objeto com simetria de inversão existe outro ponto do objeto situado à mesma distância do centro, no lado oposto. Veja a figura (a) abaixo. Embora a inversão seja uma simetria relativamente comum, é difícil achar um exemplo em que ela seja a única simetria, sem a presença de rotações ou reflexão. A figura abaixo mostra como podemos construir um objeto cujo único elemento de simetria é um centro de inversão. Corta-se um papel na forma mostrada na figura (b) e dobra-se conforme as marcas. O objeto que se obtém possui, como único elemento de simetria, um centro de inversão, mostrado como um ponto vermelho na figura (c).
Operação de translação
Essa é uma operação simples de entender mas só existe mesmo na cabeça dos matemáticos. Um objeto com simetria de translação, quando deslocado em uma certa direção, de um certo valor t, fica exatamente como era antes. Isso, evidentemente, só seria rigorosamente válido para um objeto infinito. Como não existem objetos infinitos nesse mundo, a simetria de translação é aproximada apenas em uma região limitada. A faixa abaixo tem simetria de translação pois se reproduz quando deslocada de um valor fixo para a esquerda ou direita.

Existem alguns outros elementos de simetria e suas respectivas operações, além dos que descrevemos aqui. Mas, os que vimos acima já dá para ter uma idéia de como funcionam essas operações. Na seção seguinte, vamos dar mais detalhes sobre a operação de reflexão e explicar sua importância em Física e Biologia.
A simetria dos espelhos.
Vamos falar um pouco mais sobre a simetria de reflexão. Por que essa preferência? Primeiro, porque é uma forma de simetria que tem algumas sutilezas mal entendidas pelos leigos (e até por alguns especialistas). Segundo, porque tem grande importância histórica, na Física e na Biologia. A simetria de reflexão é a simetria de um objeto colocado em frente a um espelho plano. O espelho não precisa existir, na realidade. Basta haver um plano imaginário onde ele estaria situado para reproduzir todo o objeto.

Olhando para um espelho plano comum, vemos nossa imagem, uma pessoa igual a nós, nos encarando e arremedando nossos gestos. Isso nos é familiar, mas, há uma característica da imagem refletida que precisa ser salientada: ela nem sempre pode ser superposta ao objeto refletido.
Isso fica evidente no caso de uma mão e sua imagem. A imagem de uma mão direita é uma mão esquerda. E, como é fácil constatar, uma mão esquerda não pode ser superposta sobre uma mão direita. Basta lembrar que uma luva esquerda não se ajusta a uma mão direita.
Um objeto e sua imagem refletida são ditos “enantiomorfos” (belo nome para ser decorado!). Essa palavra vem do grego: enantios=opostos e morfos=forma. A mão direita é a enantiomorfa da mão esquerda, e vice-versa. O mesmo vale para um par de sapatos, um par de luvas ou suas orelhas.

Dois objetos enatiomorfos podem, ou não, serem capazes de superposição. Uma esfera, por exemplo, pode ser superposta à sua imagem. O mesmo acontece com um cubo. Mas, não acontece com uma mão, nem com um parafuso. Para enfiar um parafuso normal na madeira devemos girá-lo no sentido horário. O parafuso enantiomorfo (imagem no espelho), teria de ser girado no sentido anti-horário, para furar a madeira. O mesmo vale para um saca-rolhas.
Essa diferença causada pela operação de simetria só ocorre na reflexão. A rotação, por exemplo, não muda em absolutamente nada o objeto simétrico sobre o qual opera. Essa curiosa característica da reflexão tem consequências espantosas na Física e na Biologia, como veremos nas seções seguintes.
Cristais simétricos e assimétricos.

Um cristal, como se sabe, deve sua forma regular a um arranjo bem ordenado de seus átomos e moléculas. Se pudéssemos ver o arranjo interno dos átomos de um cristal cúbico, como o cobre, por exemplo, veríamos algo como mostrado na figura ao lado. Os átomos se organizam de modo a ocupar os vértices de uma estrutura cúbica. Essa é uma estrutura de grande simetria. É fácil entender que uma estrutura como essa e sua imagem em um espelho podem ser inteiramente superpostas. Os enantiomorfos, nesse caso, são idênticos. Existem, porém, cristais cujas estruturas cristalinas internas não são exatamente idênticas a seus enantiomorfos. O exemplo mais comum é o quartzo.

Não vamos mostrar a estrutura interna do quartzo pois é um tanto complicada. A figura mostra dois cristais cujos arranjos internos de átomos são a imagem uma da outra. Por fora, como vemos, não dá para saber isso, pois os cristais são idênticos. Mas, se pudéssemos ver os arranjos atômicos internos, veríamos que não podem ser superpostos, do mesmo modo que uma mão direita e uma mão esquerda não se superpõem. Como distinguir um cristal de quartzo de seu enantiomorfo, se por fora eles são praticamente iguais?
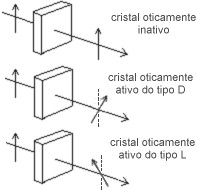
Em 1911, o físico francês Francois Arago descobriu que o quartzo (que é um cristal transparente) girava a direção de polarização de um feixe de luz que passava através dele. Não precisamos entrar em detalhe sobre essa técnica. Basta saber que é possível, observando a luz que passa pelo cristal de quartzo, distinguir entre os dois enantiomorfos. O que gira a polarização para a direita é chamado de tipo D (“dextro”) e o que gira para a esquerda é do tipo L (“levo”). O quartzo, por essa propriedade, é dito “opticamente ativo”.
O grande físico inglês, Lord Kelvin, dizia que esse tipo de cristal tem “quiralidade” (mais um nome para decorar!). Um material “quiral” tem duas estruturas possíveis, uma sendo o reflexo da outra, e girando a polarização da luz em sentidos opostos.
Como veremos na seção seguinte, esse fato tem enorme repercussão no comportamento de algumas moléculas biológicas muito importantes.
A primeira descoberta científica de Louis Pasteur.
O físico francês Jean Baptiste Biot descobriu que alguns líquidos eram opticamente ativos, isto é, giravam a direção da polarização da luz que passava por eles. Em analogia com o caso do quartzo, Biot supôs que isso se devia a uma assimetria nas moléculas do líquido. Aí, surgiu um caso intrigante com o ácido tartárico, que é obtido das uvas (coisa de francês). Algumas soluções de ácido tartárico eram opticamente ativas mas, outras não eram. Essas soluções inativas (não modificavem a polarização da luz) eram chamadas de “racêmicas”. Do ponto de vista de todas as outras propriedades físicas e químicas, porém, os dois tipos de solução eram inteiramente idênticos.

Louis Pasteur em seu laboratório
Quem resolveu esse enigma foi o jovem Louis Pausteur (22 anos, na época), que depois ficaria famoso por suas vacinas. Primeiro ele evaporou o material para obter um precipitado com cristais de ácido tartárico. Olhando esses cristaizinhos no microscópio ele descobriu algo surpreendente. Os cristais que vinham da solução opticamente ativa eram todos iguais. Mas, os cristais que vinham da solução racêmica, opticamente inativa, eram de dois tipos. Examinando com cuidado, ele viu que esses cristais eram enantiomorfos – um tipo era a imagem do outro.

Com muita paciência e cuidado, Pasteur conseguiu separar os dois tipos de cristais obtidos na solução racêmica. Depois, preparando uma solução de cada tipo de cristal, separadamente, obsrvou que ambas eram opticamente ativas. Só que uma girava a polarização da luz em um sentido e a outra girava no sentido oposto! Dai, foi fácil concluir que a solução racêmica não era ativa porque continha cristais, em igual número, girando a polarização em sentidos opostos. Uns anulavam o efeito dos outros.
O velho Biot, ao saber desse resultado, levado a ele pelo próprio Pasteur, ficou emocionado. Sua hipótese fora brilhantemente comprovada pelo jovem cientista. Essa foi a primeira grande descoberta de Louis Pasteur e tornou seu nome conhecido na comunidade científica. Dez anos depois ele faria outra descoberta na mesma área e avançaria no entendimento da quiralidade das moléculas biológicas. É o que veremos na seção seguinte.
Assimetria das moléculas biológicas.
Pasteur conseguiu transformar uma solução racêmica, opticamente inativa, em uma solução opticamente ativa, separando os cristais enantiomorfos com extrema paciência. Dez anos depois desse trabalho, ele descobriu que podia transferir essa tediosa tarefa para outro agente. Ele observou que o mofo de algumas plantas, atuando sobre uma solução racêmica, destrói exclusivamente os cristais de um dos dois tipos, deixando seu enantiomorfo incólume. Desse modo, o mofo faz o trabalho que Pasteur fez com seu microscópio e suas pinças.
Pasteur conjecturou que as moléculas do mofo também deviam ser assimétricas e se alimentavam apenas dos cristais cuja simetria combinava com a delas. Na época, sem raios-X nem microscópio eletrônico, era impossível para ele, ou qualquer outro, examinar a estrutura interna das moléculas biológicas.

Isso não impediu, porém, que outro jovem químico da época, o holandês Jacobus van’t Hoff, fizesse uma ousada hipótese. Segundo ele, as moléculas biológicas com quiralidade, isto é, com atividade óptica, teriam essa característica explicada por uma assimetria no próprio arranjo dos átomos dessas moléculas.
Uma molécula planar, isto é, uma molécula cujos átomos pertencem a um plano, é, obviamente, simétrica em relação à reflexão. O próprio plano da molécula serve de plano de espelho. Portanto, para ter atividade óptica, uma molécula tem de ser tri-dimensional. Foi essa a sacada de van’t Hoff. Ele previu a existência de moléculas tri-dimensionais e associou essa característica à atividade óptica da molécula. Veja abaixo um exemplo de molécula na forma de um tetraedro. Se as 4 pontas contiverem átomos ou radicais diferentes uns dos outros, a molécula pode ter duas formas enantiomorfas diferentes.
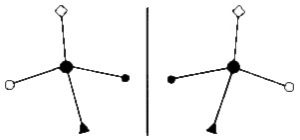
Agora, veja que coisa impressionante: todos os 20 aminoácidos que formam as proteínas encontradas nos seres vivos são assimétricos. Isto é, só existem aminoácidos naturais de uma das formas enantiomorfas, a forma “esquerda”. Isso quer dizer que o arranjo dos átomos nessas moléculas espirala de forma contrária a um parafuso ou saca-rolhas normal. Quando um aminoácido é sintetizado em laboratório, ambas as espécies (esquerda e direita) são produzidas. Nas proteínas dos seres vivos, bactérias, virus, plantas e animais, os aminoácidos são todos esquerdos (tipo L). A alanina, vista abaixo, é um exemplo de aminoácido presente em nossos corpos em sua forma esquerda (L).
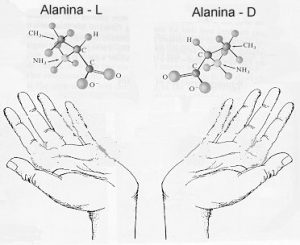
Até hoje ninguém sabe a razão desse esquerdismo da natureza. Para alguns biólogos, pode ser fruto de mero acaso na formação dos primeiros seres vivos. Começando de um jeito, não haveria mais como mudar. Talvez em outro planeta distante, os seres vivos sejam feitos de aminoácidos do tipo D. Um alienígena desses, ao nos visitar, teria de ser alimentado com uma dieta de proteínas sintéticas, feitas em laboratório. Bom apetite.
Emmy Noether e seu teorema.
As simetrias que descrevemos nas seções anteriores são do tipo geométrico, envolvendo formas no espaço. Entretanto, os matemáticos e físicos trabalham com um conceito bem mais amplo de simetria. Além da simetria espacial, existe a simetria no tempo e outras ainda mais sutís. Uma delas, a simetria da paridade, era considerada como regra indiscutível para todos os fenômenos físicos. Em 1957, quando foi demonstrado que certos fenômenos sub-nucleares não obedecem essa simetria, a comunidade ficou estarrecida. Mas, essa é uma história longa que contaremos em outra ocasião.
Nessa seção vamos falar um pouco do trabalho da matemática alemã Emmy Noether, nascida em março de 1882. Filha de uma família de judeus alemãos, ela foi educada para ser pianista e professora de línguas. Mas, seu talento para a matemática fez com que ela tentasse admissão em universidades da Alemanha. Só que o machismo na época era ainda maior do que é hoje. Mulheres tinham de pedir licença especial para frequentar os cursos, e assim mesmo, como ouvinte. Foi preciso determinação para obter um doutorado mas sua competência começou a ser notada pelos grandes da época, como Hilbert, Minkowski e Einstein. Em 1915, por pressão de Hilbert, ela foi admitida como professora na Universidade de Göetingen, mas não podia ministrar aulas oficialmente. Os cursos que ela ensinava eram anunciados com o nome de Hilbert como professor.
Foi em Göetingen que ela enunciou o teorema que passou a ser conhecido como “teorema de Noether”. Esse teorema associa cada simetria em Física a uma lei de conservação. A simetria das leis físicas em relação à translação espacial, por exemplo, implica, como resultado natural, na conservação da quantidade de movimento, ou momentum. A simetria (ou “invariância”) das leis físicas em relação ao tempo resulta na conservação da energia. Esse resultado foi levado às últimas consequências pelos físicos teóricos, desde que surgiu das mãos de Emmy Noether. Hoje, o trabalho dos físicos teóricos consiste, em boa parte, na busca e compreensão de simetrias e suas leis de conservação associadas. Algumas dessas simetrias são simples, como a rotação e a reflexão que descrevemos nas seções anteriores. Outras são muito mais complicadas, como a enigmática “simetria de calibre””, ou de “gauge”. As leis da Eletrodinâmica Quântica, enunciadas por Feynman, Tomonaga e outros, têm simetria de “gauge”. Partindo dessa hipótese de simetria, chega-se a todas as propriedades da força eletromagnética. Uma dessas propriedades, por exemplo, resulta no fato de que o transportador dessa força, o fóton, não pode ter massa.
Argumentos de simetria também orientam a descrição das forças que agem dentro do núcleo atômico e seus componentes. Essas são a “força forte” e a “força fraca” (não riam, por favor) que também devem obedecer a uma simetria de “gauge”.
Como você pode constatar, o que vimos nessas seções apenas dão uma pálida idéia (pálida, loira e de olhos azúis) da importância da simetria na ciência atual. Por essas razões, sempre que possível, retornaremos a esses temas no futuro.

