A Isostasia
Um importante conceito explicado pelo Prof. José Airton.
Introdução
As pessoas esclarecidas sempre quiseram saber como é o planeta Terra. Os sábios gregos já sabiam medir o tamanho do globo terrestre e a distância da Terra à Lua. Depois da Idade Média a procura por mais informações sobre nosso planeta intensificou-se. O pessoal queria saber qual era a forma exata da Terra, sua idade, sua massa, sua densidade e como era a dinâmica da formação e evolução das massas continentais. Nos séculos 17 e 18 essa busca de conhecimento tornou-se quase obsessiva e os sábios de então se arriscavam em incríveis empreitadas tentando obter respostas para essas questões.
A história dessas descobertas é fascinante e cheia de grandes lances. Para contá-las, convidamos o Prof. José Airton Paiva, do Departamento de Física da Universidade Federal do Ceará a escrever uma série de relatos sobre temas de Geologia. Nesse primeiro momento, ele vai nos falar sobre o conceito da Isostasia, que serve de fundamento para a compreensão de muitos fenômenos geológicos. Como veremos, o surgimento e a comprovação experimental desse conceito veio acompanhado de grandes e tortuosos debates, além de inúmeras expedições a locais remotos e perigosos, tudo temperado pelo comportamento extravagante de alguns cientistas daquele tempo que ficou conhecido como a Era do Iluminismo.
Primeiras ideias sobre a Isostasia.
Vamos começar com um conceito familiar a qualquer estudante do ensino médio, a famosa Lei do Equilíbrio Hidrostático, formulada pelo grande Arquimedes.
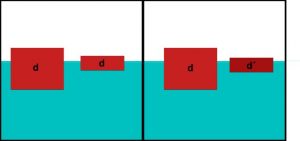
Nas figuras abaixo, vemos dois casos simples de blocos de madeira flutuando na água.
Na figura da esquerda, os dois blocos têm mesma densidade. Nesse caso, o volume submerso em cada bloco tem a mesma proporção em relação ao volume total. Isto é, se um dos blocos tem 2/3 de seu volume abaixo do nível da água, o outro bloco também tem 2/3 de seu volume mergulhado.
No caso da direita, o bloco menor é mais denso que o maior. Nesse caso, a proporção de volume submerso é maior para o bloco menor e mais denso.
Pois bem, o que é fácil de entender para blocos flutuando na água também pode ocorrer com as placas que constituem a crosta da Terra. A crosta externa está dividida em grandes blocos que “flutuam” sobre um “manto” mais profundo que, para todos os efeitos, funciona com um líquido extremamente viscoso. Isso se configura em uma espécie de equilíbrio semelhante ao equilíbrio hidrostático descrito por Arquimedes. A crosta tem densidade média menor que o manto (portanto, “flutua”) e o equilíbrio se estabelece lentamente, em tempos geológicos, por causa da alta viscosidade do manto. A esse equilíbrio, os cientistas deram o nome de ISOSTASIA e considera-se que a crosta terrestre está em um estado de “equilíbrio isostático”.

As primeiras ideias sobre o equilíbrio das camadas externas da Terra partiram de Leonardo da Vinci, o que talvez já nem surpreenda ninguém, dada a amplitude dos talentos desse italiano que viveu no século 15. Em um de seus rascunhos, Da Vinci já pensava como a Terra reagiria a uma carga extra colocada sobre sua superfície. O grande sábio especulou que a retirada de uma grande quantidade de sedimento do alto de uma montanha poderia causar sua elevação.
Isso é exatamente o que ocorre, segundo o conceito da isostasia. Por exemplo, desde que as geleiras da última glaciação, a famosa Era do Gelo, começaram a derreter, a Escandinávia começou gradualmente a subir! O degelo retirou uma enorme massa que existia sobre a crosta naquela região e o bloco como um todo começou a subir. E ainda hoje continua subindo, a uma média de 1 centímetro por ano.
Nos séculos 16 e 17, um problema básico ocupou a mente de muito cientista: qual é a massa da Terra? O raio do globo terrestre já era conhecido com alguma precisão, logo, isso equivalia a perguntar qual é a densidade da Terra. Na época, já se sabia que a densidade média das rochas encontradas na superfície estava um pouco abaixo de 3 g/cm³. Teria o planeta como um todo uma densidade semelhante a essa?
A perspectiva de se achar uma resposta para essa questão começou a melhorar depois que Sir Isaac Newton apresentou sua famosa Lei da Gravitação Universal:

Hoje, todo estudante sabe que essa força de atração exercida pela Terra sobre um objeto de massa m é exatamente o peso do objeto, P = m g, sendo g a aceleração da gravidade, medida e conhecida desde os experimentos de Galileu. Igualando as duas forças (peso e atração gravitacional da Terra), obtemos uma expressão para a aceleração da gravidade g:

onde MT é a massa da Terra, RT é seu raio e G é a chamada “constante universal da gravitação”. Portanto, para saber a massa da Terra basta medir g e saber os valores do raio da Terra e da constante gravitacional G. Medir g é fácil, qualquer aluno do ensino fundamental sabe como fazer isso e sabe que vai achar g = 9,8 m/s². O raio da Terra já era conhecido com alguma precisão desde os tempos do grego Eratóstenes. Em unidades atuais RT = 6400 quilômetros, aproximadamente. Falta só saber o valor de G.
E é aí que o bicho pega. Não é fácil medir G, ainda hoje, imagine no século 17. Basta dizer que o primeiro valor razoável de G só foi obtido 110 anos depois que Newton publicou sua lei.
Mas, antes dessa determinação de G, um inglês esquisitão conseguiu medir a densidade da Terra, como veremos a seguir.
Medindo a densidade da Terra.
A determinação da densidade da Terra foi feita, pela primeira vez, pelo lorde inglês Henry Cavendish, mais de 100 anos depois da publicação do livro Principia, de Isaac Newton. Cavendish, depois de seu experimento, declarou que medira o peso da Terra. O fato é que ele foi um dos personagens mais esquisitos da ciência daquele tempo, que aliás era cheia de gente estranha. Cavendish era de família rica mas seu talento para a investigação científica logo o levou para a pesquisa. Como era excessivamente tímido, com enorme dificuldade de convivência com outras pessoas, preferiu montar um laboratório em sua própria casa, longe dos olhos e dos palpites dos outros. Felizmente, tinha recursos financeiros para isso e conseguiu, sem sair de casa, dar valiosas contribuições para o entendimento do calor e da eletricidade. Na química, conseguiu isolar o hidrogênio e combiná-lo com o oxigênio para formar a água.

O curioso é que sua determinação da densidade da Terra foi feita usando um equipamento que ele próprio não construiu. O mecanismo foi bolado e montado por outro inglês, o pároco John Michell. Esse cientista trabalhou ativamente pesquisando o magnetismo e a gravidade. Infelizmente, morreu antes de fazer as experiências com seu aparelho para medir a constante G, mas, antes teve a sorte e o cuidado de passar suas ideias e sua montagem para Cavendish. Esse guardou o equipamento durante muitos anos e só perto do fim da vida resolveu usá-lo. E fez isso com enorme sucesso, de tal modo que até hoje o método é conhecido como a “experiência de Cavendish” e é considerado um dos mais importantes experimentos da Física.

O equipamento que Michell construiu e Cavendish usou consistia de duas grandes bolas de chumbo, cada uma com cerca de 160 quilos, presas a uma haste vertical. Outras duas esferas menores, suspensas por um fio longo e flexível, eram trazidas para perto das maiores. Surgia, então, uma força de atração entre cada par de esferas, resultando em uma torção no fio que sustentava o conjunto mais leve. O desvio angular do fio era medido e, com esse valor, era possível calcular a força gravitacional F entre as bolas. A figura mostra o detalhe de um dos pares de bolas. O fio de torção é visto no lado esquerdo da figura.

Os livros de Física costumam dizer que Cavendish mediu a constante G, mas, não foi bem isso o que ele fez. Cavendish mediu a densidade da Terra – por essa razão afirmou, “modestamente”, que pesara o planeta. Ele mediu a força gravitacional entre cada par de bolas de chumbo e mediu também o peso de cada bola. Obteve, assim, duas forças (F e P), ambas determinadas pela Lei da Gravitação de Newton. Dividindo uma pela outra, eliminou o fator G e obteve a seguinte expressão para a densidade da Terra:

Nessa equação, M é a massa da bola maior, P é o peso da bola menor, F é a força obtida pelo desvio do fio de torção e r é a distância entre as bolas. Tudo isso foi medido e com esses valores ele determinou a densidade da Terra como sendo (em unidades modernas):

NOTA: Lembre que a densidade da água é 1 g/cm³
Fazendo justiça ao feito de Cavendish, lembramos que esse foi um experimento trabalhoso que exigiu um cuidado extremo para eliminar qualquer perturbação sobre o fio de torção. A força de atração entre as bolas é muito pequena e o sistema leva tempo para se equilibrar. Cavendish montou o equipamento em uma sala isolada e fez as observações de longe, usando um telescópio para medir o desvio do fio de torção sem perturbá-lo. As medidas levaram quase um ano para serem concluídas e, malgrado todas essas dificuldades, o valor obtido por Cavendish foi excelente, apenas cerca de 1% diferente do usado atualmente.
Ora, a densidade média das rochas encontradas na crosta terrestre é de apenas 2,7 g/cm³. Essa grande diferença indicava que o interior da Terra não é homogêneo e sua densidade aumenta com a profundidade.
Apesar do sucesso das medidas de Cavendish, os sábios da época não estavam satisfeitos. Além de quererem comprovar esse resultado usando outras técnicas, queriam também saber a forma exata do planeta. E foi esse objetivo que levou alguns a aventuras incríveis, como vamos ver a seguir.
Medindo a forma da Terra.
Todo mundo esclarecido, depois das descobertas marítimas e do avanço da ciência nos séculos 15 e 16, já sabia que a Terra é uma grande bola girando em torno do Sol. Mas, seria essa bola uma esfera perfeita ou teria algum achatamento? Isaac Newton, em seu livro, os Principia, deu um palpíte: a Terra deveria ser um pouco achatada nos polos e ligeiramente barrigudinha no equador, por causa de seu movimento de rotação em torno do eixo polar.

Se Newton estivesse certo, o comprimento de um grau medido em algum meridiano do planeta seria maior perto dos polos que perto do equador. A figura ao lado mostra esse caso com um certo exagero para facilitar a visualização. Acontece que Newton era inglês e, nos séculos 17 e 18 a rivalidade entre a Inglaterra e a França não se continha na política e transbordava para a ciência. E na França havia gente influente que garantia que a Terra era achatada, não nos polos mas no equador. Os astrônomos mais importantes da França eram Giovanni e Jacques Cassini, pai e filho, que fizeram algumas medidas do comprimento de um grau perto de Paris, em 1700, e afirmavam que Newton estava redondamente enganado. Baseados em suas medidas, os Cassini afirmaram que o raio polar da Terra era maior que o raio equatorial. Isso era o contrário do que Newton tinha previsto.

Os franceses ficaram felizes em contradizer o grande Newton, mas, pelo menos foram cientificamente honestos e resolveram organizar duas expedições para tirar a dúvida. Ainda mais porque havia um cientista francês que apoiava abertamente a opinião de Newton. Esse dissidente era Pierre Louis Moreau de Maupertuis, mais um dos inúmeros personagens pitorescos que povoavam a ciência europeia daqueles tempos. Quem mais gozou com a cara de Maupertuis foi Voltaire, apesar de concordar com ele na controvérsia sobre a forma da Terra. Voltaire era fã de Newton mas não se cansava de satirizar seu conterrâneo. Talvez até gostasse dele, mas Voltaire era do tipo que preferia perder um amigo que uma piada.
Para solucionar essa controvérsia sobre a forma da Terra, a Académie Royale des Science, por ordem de Louis XV, mandou várias equipes de cientistas para diferentes pontos do planeta, com o objetivo de medir com precisão o comprimento do arco correspondente a 1 grau do meridiano. Uma delas, chefiada por Charles-Marie de La Condamine, veio para a América do Sul e percorreu trilhas muito acidentadas no Peru e no Equador. La Condamine apoiava os Cassini e esperava encontrar evidências para o achatamento da Terra no equador. Outra, chefiada exatamente por Pierre Maupertuis, dirigiu-se ao Ártico, para a Lapônia, na Finlândia. Ambas foram recheadas de contratempos e dificuldades. Na Lapônia, Maupertuis e sua turma enfrentaram mosquitos, problemas com as renas e um frio de lascar só aplacado um pouco pelos 400 litros de aguardente que tiveram o cuidado de levar na bagagem. Maupertuis, que era um mulherengo, logo se ligou a duas lapãs que o acompanharam durante toda a missão e acabaram indo com ele para Paris. Mais um motivo para as gozações de Voltaire.
Na América do Sul, para onde vieram La Condamine e Pierre Bouguer, as coisas ainda foram mais difíceis. O terreno que escolheram para suas medidas era extremamente acidentado, a altitude era um desafio e os nativos não eram muito amistosos com a equipe de exploradores. E, pior: os resultados que obtiveram com grande sofrimento apoiavam Newton e o achatamento nos polos. La Condamine e Bouguer acabaram brigando entre si e voltaram à França depois de vários anos, derrotados e insatisfeitos.
Portanto, o resultado das medidas das duas equipes, obtidos com enorme custo, foi desastroso para os Cassini. Ficou mesmo comprovado que a Terra é achatada nos polos e cerca de 45 quilômetros mais bojuda no equador. Quando Maupertuis voltou (com suas lapãs), Voltaire, como sempre, não perdoou e escreveu uma poesia que acaba assim: “Vous avez confirmez dans les lieux pleins d´ennui – Ce que Newton connut sans sortir de chez lui.” (“Você confirmou em cantos cheios de desgosto – O que Newton sabia sem sair de seu posto.”)

Nessa altura, vale a pena conhecer as técnicas usadas por esses cientistas para medir o comprimento de um arco meridiano. Como a distância entre os dois pontos extremos era muito grande, não dava para medir essa distância diretamente com uma trena, é claro. Ainda mais levando em conta que o terreno era cheio de altos e baixos, com pântanos e mata cerrada pelo meio. Por essa razão eles usavam a técnica da triangulação. Esse processo consiste em estabelecer uma rede de triângulos começando no ponto inicial e terminando no final. Em cada triângulo, basta medir um dos lados (o que for mais conveniente, é claro) e os ângulos em cada ponta desse lado. Dessa forma, como todo aluno de geometria sabe, os outros dois lados do triângulo ficam determinados sem precisar medí-los diretamente. Passando de triângulo em triângulo acaba-se obtendo a distância entre os pontos A e B com boa precisão. A figura ao lado, adaptada do mapa usado por Maupertuis, mostra como ele mediu a distância entre dois pontos perto de Tornio, no círculo ártico. O resultado que ele achou mostrou que o comprimento do grau meridiano nessa posição era cerca de 1500 metros maior que o medido próximo ao equador. Portanto, Maupertuis estava correto, Newton tinha razão e a Terra é mesmo achatada nos polos. A tabela abaixo mostra os resultados obtidos por Maupertuis em Tornio, por outros em Paris e por La Condamine em Quito. Os valores estão em uma unidade chamada “toise”, utilizada antes que a Revolução Francesa inventasse o sistema métrico. 1 toise equivale a 1,9 metros.

Pierre Bouguer, membro da equipe de la Condamine não ficou convencido dos resultados obtidos e pôs a culpa no colega. Por essas alturas, os dois já estavam de ponta um com o outro. Bouguer passou a dizer que os resultados que tinham obtidos estavam viciados por causa das enormes montanhas no Equador, enquanto que no Ártico o relevo era plano. Segundo ele, a massa das montanhas nas vizinhanças de Quito estariam causando erros na determinação das posições escolhidas para as triangulações. Por essa razão, em passagem pelo Peru, ele resolveu medir a densidade média da Terra a partir da atração gravitacional entre uma montanha e um pêndulo. Os resultados que obteve e suas importantes consequências serão relatados no próximo capítulo.
Modelos de Isostasia.

Pierre Bouguer, aquele mesmo que veio para a América do Sul com La Condamine para medir o comprimento do arco meridiano, notou algo esquisito quando tentava medir a densidade de uma montanha. Como muitos sábios daquele tempo, Bouguer adorava usar pêndulos em suas medidas. O célebre Prof. Girassol, personagem da série Tintim criada pelo desenhista belga Hergé, é um exemplo desse estereótipo de cientista dos séculos passados, sempre com um pêndulo na mão. Pois bem, Bouguer usou um pêndulo parado – isto é, um fio de prumo – em sua tentativa de medir a densidade média de uma montanha.

A ideia era simples. Normalmente, um fio de prumo indica a vertical do lugar, isto é, deve apontar na direção do centro da Terra. Perto de uma montanha, porém, o fio de prumo deveria se deslocar em relação à vertical, aproximando-se um pouco da montanha. Bouguer fez alguns cálculos e verificou que, medindo esse desvio relativo, poderia obter uma estimativa para a relação entre a densidade média da montanha e a densidade média da Terra. Só que os resultados foram surpreendentes e inesperados. Bouguer achou valores muito pequenos para a densidade da montanha, inconsistentes com o que esperava de sua estimativa para a massa da montanha. Em algumas medidas, o pêndulo se desviava para longe da montanha! Em outras palavras, a montanha parecia ser menos densa que a planície. Hoje, esse tipo de resultado é conhecido como “anomalia de Bouguer”. E, lembrando o que vimos no início dessas páginas, deu início ao conceito de isostasia.
A primeira explicação para esses curiosos resultados veio em 1885, quando George Airy e John Pratt propuseram, independentemente um do outro, modelos para a variação de densidade observada. Em 1889, o geólogo americano Clarence Dutton propôs o termo isostasia segundo o qual existe um balanceamento da crosta terrestre. Segundo essa ideia, a camada superficial da Terra, relativamente rígida, repousa sobre um substrato mais denso. Parecido com os blocos de madeira flutuando sobre a água. Hoje, sabe-se que essa camada corresponde à crosta e a parte do manto superior, integrando o que chamamos de litosfera. O substrato mais profundo e denso é o manto sólido que se comporta como um fluido viscoso que escorre em tempos geológicos e no qual ocorrem deformações plásticas.
Os modelos de Airy e de Pratt têm diferenças fundamentais. No modelo de Airy, as densidades nas diversas partes da crosta são aproximadamente iguais. As montanhas são mais altas por terem raízes mais profundas. Já no modelo de Pratt, a camada superior rígida é composta de blocos que têm, aproximadamente, a mesma profundidade, mas são de densidades diferentes. Nesse caso, as montanhas são mais elevadas por serem compostas de rochas de menor densidade que as existentes nas regiões vizinhas.
Como seria de se esperar, hoje se sabe que os dois modelos co-existem. As montanhas são mais espessas, como no modelo de Airy, mas, as densidades podem variar lateralmente, como no modelo de Pratt. Ambos os modelos concordam que, em um nível profundo existe uma pressão constante ao longo de vastas regiões, chamado de nível de compensação. A pressão nesse nível seria dada pela fórmula da pressão hidrostática, ρ g h.

Os dois modelos explicam de forma satisfatória várias observações sobre a crosta terrestre. Os continentes são mais elevados que a crosta no fundo do mar porque são menos densos. E, sendo menos densos, precisam ser mais espessos para compensar o equilíbrio nas profundezas. Nas regiões montanhosas, a crosta é mais profunda. Realmente, os dados atuais concordam com essas suposições. A densidade média da crosta continental (cerca de 2,7 g/cm³) é menor que a densidade média da crosta oceânica (cerca de 3,0 g/cm³).
Modelos mais recentes, como o proposto pelo geólogo holandês Felix Venning, descreve a crosta como uma placa elástica que pode se deformar para distribuir as cargas topográficas sobre uma grande região. Na verdade, podemos dizer que o assunto todo ainda é objeto de pesquisa. A hipótese básica da isostasia, segundo a qual a crosta flutua em equilíbrio dinâmico sobre um substrato viscoso pode ser considerada bem sucedida e serve de molde para modelos cada vez mais complexos que aparecem nas revistas especializadas.
Autor: José Airton Paiva – Departamento de Física da UFC

