Os Matemáticos Leonhard Euler, Karl Gauss e Evariste Galois.
Resolvemos prestar uma homenagem aos matemáticos, falando sobre a vida e a obra de dois dos maiores que já passaram por esse vale de lágrimas, o suíço Leonhard Euler e o alemão Karl Friedrich Gauss e de um menos influente mas muito mais romântico, Evariste Galois . As histórias desses expoentes da espécie humana, vista por quem sabe apreciá-las, é tão emocionante quanto a história de qualquer astro do esporte. Não temos a intenção de contá-las aqui, apenas oferecemos um aperitivo para despertar a curiosidade de nossos visitantes sobre esses gigantes e seus colegas de todos os tempos.
Leonhard Euler: produziu suas maiores obras quando já estava velho e cego.
Leonhard Euler (pronuncia-se “Óiler”) nasceu na Basiléia suíça em Abril de 1707. Seu pai era ministro religioso e 
queria que o filho também seguisse a carreira clerical. No entanto, bem cedo o talento matemático de Euler foi descoberto por Johannes Bernouilli que lhe emprestava livros e tirava dúvidas. Como o pai de Leonhard era amigo e ex-colega de Bernouilli não foi difícil convencê-lo que a verdadeira vocação do filho era a matemática.
Desse modo, com menos de 20 anos, Euler foi nomeado professor de matemática da Academia de Ciências de São Petersburgo, criada por Catarina, viúva de Pedro, o Grande. Em 1730, Euler passou para a cátedra de física. Em 1734, casou com Katharine Gsell e com ela teve 13 filhos. A facilidade de Euler com a matemática era tão grande que muitos de seus artigos foram compostos enquanto ele brincava com os filhos. Costumava dizer, de brincadeira, que seu lápis era mais inteligente que ele próprio.
Em 1738, Euler começou a perder a visão de um dos olhos e o outro também não ia muito bem. Sua visão foi gradualmente se deteriorando mas esse infortúnio não diminuiu em nada sua capacidade de trabalho.
Depois de trabalhar por mais de dez anos na Rússia, Euler aceitou o convite de Frederico, o Grande, rei da Prússia e
foi trabalhar em Berlim. Frederico era um dos chamados “déspotas esclarecidos”, comuns na época. Eram soberanos amigos das artes e das ciências, patrocinadores de filósofos e cientistas. No entanto, apesar de ter sido convidado pessoalmente pelo rei, Euler nunca se deu muito bem com ele. Frederico preferia o convívio de filósofos cheios de verve, como Voltaire, e achava Euler um casca grossa. Assim mesmo, Euler trabalhou em Berlin por 26 anos e lá produziu uma grande quantidade de trabalhos que lhe deram fama e prestígio. Finalmente, em 1766, quando os problemas profissionais com Frederico começaram a se agravar, Euler resolveu voltar para São Petersburgo, o que deixou o monarca furioso.
De volta à Rússia, porém, os problemas de visão de Euler começaram a se agravar ainda mais. Em 1771, depois de uma operação de catarata mal sucedida e outras complicações, o grande matemático ficou completamente cego.
Apesar desse infortúnio, e apesar de estar com mais de 60 anos de idade, foi nessa época que Euler produziu boa parte de seus trabalhos mais importantes em matemática e física. É claro que tinha ajuda, principalmente de seus filhos Johann, que era físico, e Christoph, que era engenheiro, além de seus colegas e alunos da Academia.
Euler morreu de repente em Setembro de 1783, aos 76 anos. Em vida, publicou mais de 500 trabalhos. Durante mais de 50 anos após sua morte, a Academia publicou, postumamente, seus trabalhos ainda inéditos, que somaram mais de 400.
Tarefas de Leonhard Euler na Academia de Ciências.
Em Berlim, Euler trabalhou na Academia de Ciências que era dirigida por Maupertuis, de quem se tornou grande 
amigo. Aliás, Euler tinha tanta facilidade para fazer amigos quanto para fazer matemática. Agora, trabalhar em uma Academia mantida por um rei daquela época não era essa coisa folgada que é trabalhar em uma universidade de hoje. Veja quais eram algumas das responsabilidades de Euler como membro da Academia de Berlim.
Cabia a ele uma grande quantidade de tarefas administrativas: supervisionar o observatório astronômico e o jardim botânico; cuidar das finanças; selecionar os empregados a serem contratados; produzir mapas e calendários e tratar de vendê-los para ajudar nas despesas da instituição.
E, além dessas tarefas de administrador, Euler era encarregado, pelo rei, de projetar canais e de cuidar da instalação hidráulica do palácio. Trabalhava, também, como editor científico das publicações da Academia e como consultor da loteria do reino e da previdência oficial. Um cara polivalente como esse faria o maior sucesso em qualquer governo de hoje.
Pois apesar de todas essas incumbências, Euler ainda conseguia produzir uma quantidade incrível de trabalhos de matemática e física da maior qualidade. Nos 25 anos em que morou em Berlim, Euler publicou cerca de 380 artigos.
E ainda tem gente, em nossas universidades, reclamando da carga didática e dizendo que ela atrapalha sua pesquisa…
Alguns trabalhos científicos de Leonhard Euler.
Euler foi um dos criadores da moderna análise matemática. Em Física, estudou os fluidos, a dinâmica dos corpos, a elasticidade, a acústica, a teoria ondulatória da luz e a hidráulica. Publicou até vários artigos sobre música. Vejamos alguns exemplos dos trabalhos de Euler:
*** Um problema que desafiou matemáticos do calibre de Leibnitz e dos Bernouilli era achar o valor da seguinte soma:
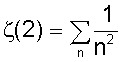
quando n tende para o infinito. Essa soma é chamada de função zeta.
Em 1735, com apenas 22 anos, Euler mostrou que
Não se deu por satisfeito e mostrou que:
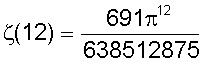
** Em 1738, Euler demonstrou a famosa fórmula:
eix = cos x + i sen x
que relaciona as funções trigonométricas com a exponencial.
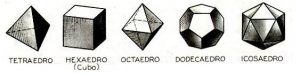
*** Em geometria, achou uma relação simples entre o número de faces (F), o número de vértices (V) e o número de arestas de um poliedro regular. Essa relação é: F + V = A + 2.
Com ela é possível e relativamente fácil demonstrar que só existem cinco poliedros regulares, que são mostrados na figura abaixo. Verifique a fórmula acima para cada um deles.
*** O famoso problema da braquistócrona, proposto por Johann Bernouilli, levou Euler a produzir um enorme avanço no cálculo das variações, depois desenvolvido extensivamente por Lagrange. Esse problema da braquistócrona está descrito com mais detalhe em nossa seção de SUGESTÕES PARA FEIRAS DE CIÊNCIAS.
Aliás, a fundamental equação de Euler-Lagrange:
é a base do estudo da dinâmica em qualquer curso de física.
*** Por fim, existe uma fórmula que é considerada por muitos como a mais bela de toda a matemática. Ela foi descoberta por De Moivre e desenvolvida por Euler. É a seguinte:
Como vemos, em uma única, simples e compacta expressão estão combinados os cinco números mais importantes da matemática.
Euler e as Pontes de Konigsberg.
Para dar um exemplo curioso do trabalho de Euler vamos relatar o caso das Pontes de Konigsberg, problema que ele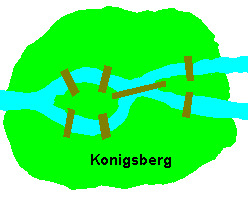
resolveu em 1735. Esse problema e sua solução praticamente inauguraram uma nova área da matemática chamada Topologia e deram origem ao estudo dos “grafos”, que estão muito na moda com os caras que se dedicam às redes em física estatística.
Consta que em Konigsberg, Alemanha, um rio que passava pela cidade tinha uma ilha e, logo depois de passar por essa ilha se bifurcava em dois ramos. Nessa região existiam sete pontes, como mostra a figura.
O povo queria saber se era possível andar por toda a cidade de tal modo que cada ponte fosse atravessada exatamente uma vez. Pois bem, faça uma cópia desse mapa e tente achar uma trajetória com esse requisito.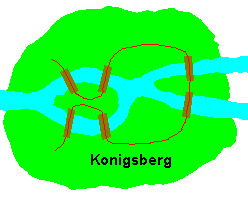 
Depois volte a ler este texto.
Conseguiu? Não? Nem Euler! Na verdade, esse problema, da forma como foi colocado, não tem solução. Não existe nenhuma trajetória passando pelas pontes de Konigsberg que satisfaça o esquema exigido. Curiosamente, se o número de pontes fosse apenas seis, como mostrado na figura, haveria uma solução bem simples.
Vejamos como Euler atacou o problema. Para começar, ele notou que o desenho fica mais simples trocando as áreas de terra por pontos (os VÉRTICES) e as pontes por arcos. Veja o mapa das pontes de Konigsberg e o 
esquema simplificado de Euler.
O problema agora consiste em percorrer todos os arcos, passando por cada um apenas uma vez, sem levantar o lápis do papel.
Agora, veja: cada vértice tem um número ÍMPAR de arcos chegando a ele (3 ou 5). Considere, por exemplo, um vértice com três arcos, como o superior. A primeira vez que você chegar a esse vértice através de um dos arcos, poderá sair dele por outro dos dois restantes. Mas, quando chegar novamente nesse vértice pelo terceiro arco, morreu! Não há como sair dele sem retraçar um arco.
Existem duas possibilidades que dão certo, no entanto. 1) Se esse vértice com 3 arcos for o último, alcançado pela primeira vez no final da viagem. Nesse caso, os outros dois arcos servem apenas para atravessar uma ponte e voltar pela outra. 2) Se você começar por esse vértice e depois, em um momento posterior, chegar de volta a ele, sair e não mais voltar.
Portanto, um vértice com um número ímpar de arcos tem de ser o primeiro ou o último da trajetória. Isto é, podem haver, no máximo, dois vértices com um número ímpar de arcos ligados a eles.
No caso das pontes de Konigsberg, existem quatro vértices com um número ímpar de arcos, logo, esse caso não tem solução.
Na teoria de grafos, uma área da topologia provavelmente iniciada com esse problema, um caminho completo com as propriedades descritas acima de não retraçar nenhum arco é chamado de TRAJETÓRIA de EULER
Será que existe alguma trajetória de Euler para o gráfico ao lado? Se existir, como ela é?
Karl Friedrich Gauss: seu gênio começou a assombrar o mundo quando ele tinha apenas sete anos.
Karl Friedrich Gauss nasceu na Alemanha, de família pobre. Na escola, aos sete anos, o professor pediu aos alunos que 
calculassem a soma dos inteiros de 1 a 100. Coisa típica de professor que quer fazer a turma ficar quieta enquanto lê o jornal. Pois Gauss deu a resposta certa em poucos minutos. Ele notou que 1+100=101, 2+99=101 etc. Isto é, bastava somar 50 números iguais a 101. Portanto, a soma era 50 x 101 = 5050. A fama do moço começou aí.
Aos 19 anos, achou um método de construir o heptadecágono (veja mais adiante). Esse era um problema que os geômetras tentavam desde o tempo dos gregos.
Os trabalhos de Gauss cobriram praticamente toda a matemática da época. Provou o chamado Teorema Fundamental da Álgebra que diz que todo polinômio tem uma raiz da forma a + bi.
Em Física, deu grandes contribuições ao campo do magnetismo, área em que trabalhou fazendo parceria com Weber. Hoje, a unidade de campo magnético pode ser o gauss ou o weber/m2.
Em 1801, foi descoberto um asteróide que depois recebeu o nome de Ceres. Logo, vários astrônomos se dedicaram a tentativa de calcular a órbita desse asteróide. Infelizmente, pouco depois de sua descoberta, o asteróide escondeu-se atrás do Sol, de modo que os dados obtidos de suas posições eram muito poucos. Assim mesmo, muitos publicaram seus resultados, inclusive Gauss, só que as previsões do alemão eram bem diferentes das dos demais. Pois quando o asteróide reapareceu, alguns meses depois, sua posição coincidia perfeitamente com a previsão de Gauss. Hoje sabemos que Gauss usou um método que desenvolvera, chamado de método dos mínimos quadrados, que se tornou, desde então, ferramenta importante do trabalho em ciências experimentais.
Gauss gostava muito de trabalhar com geometria diferencial, tendo inventado o importante conceito da curvatura dupla, hoje conhecida como curvatura de Gauss.
Em 1820, inventou o heliótropo, instrumento que usa a reflexão da luz do Sol para medidas geodésicas. Pensou até em usá-lo para se comunicar com hipotéticos habitantes da Lua.
Em 1833, com a ajuda de Weber, construiu o primeiro telégrafo. Esse aparelho é mostrado na figura abaixo.
Gauss sabia tudo sobre estatística. Mostrou que os erros nas medidas experimentais costumam seguir uma distribuição em forma de sino, hoje chamada de distribuição gaussiana (ver adiante). Sua engenhosidade em tratar com esses assuntos levou-a, no final da vida, a especular na Bolsa de Valores. Foi tão bem sucedido nessa atividade que morreu rico.
A Lei de Gauss e a distribuição gaussiana.
A Lei de Gauss da Eletricidade é bem conhecida de todo estudante de Matemática ou de Física. Em palavras, ela diz:
“O fluxo de linhas de campo através de uma superfície fechada é proporcional à massa (ou carga) dentro dessa superfície.”
Escrevemos carga ou massa pois a Lei de Gauss serve tanto para o campo elétrico quanto para o campo gravitacional.
O que pouca gente sabe é que essa idéia de Gauss resolveu um enigma que atormentou Newton por vários anos.
A questão era a seguinte.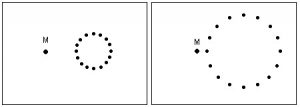 
Imagine um aglomerado esférico de pequenas massas, todas iguais, a uma certa distância de outra massa pequena M. É claro que a massa M sofrerá a atração gravitacional das massinhas do aglomerado esférico.
Agora, suponha que o aglomerado esférico se expanda uniformemente, aumentando de raio. Algumas massas se aproximam de M e outras se afastam. A pergunta é: com essa expansão a força gravitacional sobre M aumenta, diminui ou fica constante?
A resposta correta é: fica constante. Newton sabia disso mas não sabia como provar de forma simples e convincente.
Gauss, com sua lei, mostrou que é fácil provar essa afirmação.
Vamos, por simplicidade, traçar linhas de campo saindo de cada massa do aglomerado como retas radiais (Fig. A). Consideremos uma superfície esférica S, imaginária, passando pela massa M. Essa é a chamada “superfície de Gauss”. A força sobre M depende do número de linhas que atravessa S (o “fluxo”).
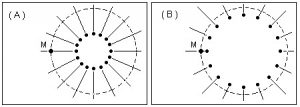
Ora, esse número é o mesmo, antes ou depois do aglomerado se expandir (Fig. B). Logo, a força sobre M não muda com a expansão.
Newton não teve essa inspiração (Gauss viveu muito depois dele) e teve de inventar o cálculo infinitesimal para resolver esse enigma que o perturbava.
Outra descoberta importante de Gauss foi como se distribuem os desvios em uma série de medidas experimentais.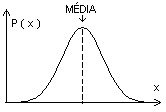 
Ele mostrou que esses desvios se distribuem em torno do valor médio segundo uma curva em forma de sino. Essa é a chamada “distribuiçao gaussiana”.
É realmente impressionante observar, experimentalmente, que os desvios em torno do valor médio se distribuem com uma forma tão regular. Essa experiência é sugerida em uma seção de nossas SUGESTÕES PARA FEIRAS DE CIÊNCIAS.
Gauss e o polígono de 17 lados.
Desde o tempo dos antigos gregos, o passatempo favorito dos geômetras era tentar desenhar polígonos regulares usando apenas régua e compasso. Os gregos sabiam desenhar o triângulo (3 lados), o quadrado (4 lados) e o pentágono (5 lados). E, como sabiam dividir um ângulo em duas partes iguais, podiam também obter todos os polígonos com número de lados dobrado, a partir desses três.
Um grande desafio, desde esses velhos tempos, consistia em desenhar um polígono de 17 lados, o heptadecágono. Pois bem, em Março de 1796, Karl Gauss, com apenas 19 anos, conseguiu essa façanha. E não ficou só nisso. A seguir, mostrou como desenhar qualquer polígono regular de n lados, desde que n seja um número primo da forma 2^2^k + 1, os chamados “primos de Fermat”.
Para mostrar a vocês como se desenha um heptadecágono, damos a seguir a construção de Richmond, datada de 1893.
1) Desenhe uma circunferência com centro em O. Essa será a circunferência principal. Escolha um vértice qualquer V nessa circunferência.
2) Localize o ponto A na circunferência tal que OA seja perpendicular a OV.
3) Localize o ponto B sobre OA tal que OB = OA /4.
4) Localize o ponto C sobre OV tal que o ângulo OBC seja OBV/4.
5) Localize o ponto D sobre a extensão de OV tal que DBC seja 45o.
6) Localize o ponto E onde a circunferência que passa por D e V corta OA.
7) Desenhe a circunferência com centro em C passando pelo ponto E.
8) Localize os pontos F e G onde essa circunferência corta OV.
9) Desenhe retas perpendiculares a OV começando nos pontos F e V.
10) Essas retas cortam a circunferência principal nos pontos V3 e V5. Os pontos V3 e V5 são o terceiro e quinto vértices do heptadecágono regular. O ponto V é o vértice zero.
Os demais vértices podem ser achados a partir desses três por divisões sucessivas de ângulos.
Gauss considerava essa construção sua maior proeza na matemática. Consta que ele queria que um heptadecágono fosse desenhado em seu túmulo, como a esfera inscrita em um cilindro foi desenhada no túmulo de Arquimedes. Infelizmente, esse seu desejo não foi cumprido. Em compensação, o heptadecágono está desenhado no monumento em sua homenagem que existe em Brunswick, sua cidade natal.
Evariste Galois e sua vida atribulada.
Evariste Galois nasceu em Bourg La Reine, perto de Paris, onde seu pai chegou a ser prefeito. Desde menino, Evariste
foi um cara complicado e sua esquisitice aumentou ainda mais quando seu pai cometeu suicídio. Ao que parece, um padre da cidade inventou umas mentiras que atingiram a reputação do velho e ele não resistiu às pressões. Os liberais da cidade, amigos do falecido, fizeram um tremendo escarcéu, chegando a apedrejar o padre caluniador. Esses acontecimentos só fizeram aumentar a revolta no espírito do jovem Galois, já naturalmente anticlerical. Pouco depois da morte do pai, Evariste se submeteu a um teste de admissão à famosa Ecole Polytechnique mas não foi aceito. Consta que chegou a jogar um apagador na cabeça de um dos examinadores que insistia em dizer besteiras. Desse jeito fica difícil ser aprovado em um concurso. Aliás, essa foi a tônica durante toda a curta vida do rapaz. Todo mundo reconhecia nele um gênio da matemática mas pouca gente conseguia conviver amigavelmente com ele. Por fim, Galois teve de se conformar em cursar a Ecole Normal, menos prestigiosa que a Poly mas também respeitada pela comunidade científica.
Pra complicar ainda mais, o moço Galois era um tremendo azarado. Seu primeiro trabalho importante, quando ele tinha cerca de 18 anos, foi encaminhado por Cauchy à Academia Francesa, para concorrer a um prestigioso prêmio. O manuscrito foi parar nas mãos de Fourier, que era o secretário da Academia, e o grande Jean Baptiste achou de falecer logo depois de receber os papéis. Resultado: o artigo se perdeu e nunca foi considerado para o prêmio.
Por esse tempo, como se não bastassem suas atribulações profissionais, Galois começou a se envolver em política. E, como não podia deixar de ser, foi logo para a oposição, afrontando o rei Luiz Felipe, que depois virou nome de um delicioso bolo. Por essas e outras, acabou sendo expulso da Ecole Normal e passou a ter dificuldades financeiras. Em 1832, foi preso e chegou a tentar o suicídio na cadeia mas for salvo pelos colegas. Quando uma epidemia de cólera se espalhou por Paris os presos foram levados para um hospital nos arredores da cidade. Lá, Galois se apaixonou por Stephanie du Motel, filha de um dos médicos. Mas a moça, apesar do sobrenome, não topou transar com um pirado daquele tipo e deu-lhe um gelo. Talvez por causa dessa desilusão amorosa, Galois se meteu em mais uma confusão e foi desafiado para um duelo com um tal de d´Herbinville. Conta a lenda que, na noite anterior ao duelo, Galois trabalhou febrilmente em sua teoria sobre os grupos e as equações, tentando completar seu manuscrito. Em um canto do papel, escreveu: “Há algo a completar nessa demonstração. Eu não tenho tempo”.
Passar a noite produzindo matemática não é indicado para quem vai duelar bem cedo na manhã seguinte. Galois foi ferido no duelo e morreu, com menos de 21 anos de idade. Sobre esse duelo, pouco se sabe. Não se sabe nem a razão. Houve quem dissesse que a briga foi em torno de Stephanie mas isso pode ser palpite de quem gosta de romantizar as coisas. Houve quem visse uma conspiração política. O fato é que Galois estava de saco cheio com a vida. Rejeitado no amor, sem grana no bolso, perseguido pelo governo e sem uma aceitação clara de seus trabalhos pela comunidade matemática, é até provável que o duelo tenha sido uma espécie de suicídio premeditado.
De qualquer modo, ninguém, depois que ele morreu, pôs em dúvida a enorme importância da pesquisa e dos resultados que ele alcançou. Galois foi o primeiro cara a entender direitinho a nascente teoria dos grupos finitos. Ele usou muito bem essa teoria para mostrar quais são as condições para se obter soluções para equações polinomiais por radicais. Anos depois, a teoria de grupos, que por muito tempo foi objeto de estudo apenas de matemáticos puros, começou a ter aplicações na solução de problemas físicos. E, como costuma acontecer, os físicos deram novos impulsos à teoria que teve Galois como um dos pioneiros.
A teoria de grupos e as equações polinomiais.
Não dá para explicar a teoria de Galois nesse espaço pois ela é muito técnica. Mas, é possível dar uma idéia do que é a teoria de grupos.
Imagine uma coleção de n elementos que serão simbolizados por n letras diferentes: A, B, C, … Essa coleção será um grupo se forem satisfeitas as seguintes quatro condições:
1) Existe uma operação que será chamada de “produto” entre dois elementos quaisquer e que tem a seguinte propriedade: o produto de dois elementos do grupo também é um elemento do grupo. Exemplo: o produto A.B entre os elementos A e B do grupo é outro elemento do grupo, por exemplo, C. Isto é, A.B = C.
2) Existe um elemento do grupo, que será chamado de IDENTIDADE e será simbolizado pela letra I, que tem a seguinte propriedade: o produto de I por qualquer elemento do grupo resulta no próprio elemento. Exemplo: I.A = A.
3) Os produtos são “associativos”, isto é, A.(B.C) = (A.B).C = A.B.C.
4) Todo elemento do grupo tem um inverso que também é um elemento do grupo tal que o produto do elemento por seu inverso resulta no elemento identidade. Chamando o elemento inverso de A de A-1, temos: A.A-1 = I.
Veja um exemplo de grupo. Os números inteiros, negativos, positivos e o zero, formam um grupo. Para esse grupo, a operação produto é a soma usual entre números (+). O elemento identidade é o zero. E o inverso de cada elemento é seu negativo. Verifique que todos os 4 requisitos são satisfeitos por essa coleção.
Um grupo pode ser formado por qualquer tipo de elementos, não necessariamente numéricos. Um exemplo interessante, que foi um dos casos utilizados por Galois é o grupo das permutações
Permutar, como todo mundo sabe, consiste simplesmente em trocar posições. Então, vamos considerar os três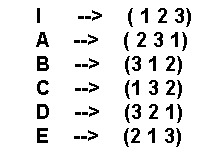 
algarismos, 1, 2 e 3, e vamos ver quantas permutações podemos fazer com eles. É fácil; uma rápida tentativa mostra que só temos 6 permutações possíveis. (Qualquer aluno de segundo grau sabe que o número de permutações de n elementos é n!). Essas 6 permutações estão listadas na tabela ao lado. A primeira consiste em não permutar nada. Isto é, a ordem 1 2 3 continua sendo 1 2 3. Essa é, evidentemente, a permutação identidade, ou I, na nossa notação. A segunda permutação, que chamaremos de A, troca o 1 por um 2, troca o 2 por um 3 e troca o 3 por um 1. E assim por diante para as demais permutações.
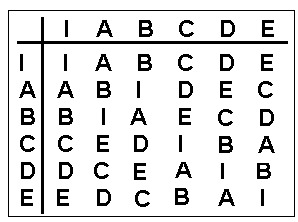
Pois bem, podemos mostrar, facilmente, que essas 6 operações de permutação, formam um grupo. Note que os elementos do grupo não são os três números, são as 6 operações de troca de números. Para ver que essas 6 operações formam um grupo de 6 elementos, basta verificar que elas satisfazem os quatro requisitos que um grupo precisa cumprir. O primeiro já está satisfeito: a operação não trocar nada é o elemento identidade, I. Vejamos o segundo quesito que envolve os produtos. Um produto de duas permutações, A.B, por exemplo, consiste em fazer, inicialmente, as trocas indicadas por B e logo após fazer as trocas indicadas por A sobre o resultado da troca inicial. Nesse exemplo (A.B), a operação B troca os números 1 2 3 pelos números 3 1 2, como mostra a lista acima. Logo após, a operação A sobre os números 3 1 2 leva para a seqüência 1 2 3. (Verifique isso usando a lista acima). Portanto, o produto AB leva a seqüência 1 2 3 de volta a ela mesma. Isto é, o produto A.B é igual ao elemento identidade, I. Desse modo, você pode se divertir e verificar que todos os produtos de duas operações leva a outra operação já listada. Portanto, o segundo requisito está satisfeito.
Deixamos para você a tarefa de verificar que os outros dois requisitos também são atentidos pela coleção de 6 operações de permutação de 3 algarismos. Logo, essa coleção é um grupo. Damos abaixo a tabela de produtos desse grupo. Lendo essa tabela você verifica, por exemplo, que o produto C.D é igual a B, mas, o produto D.C é igual a A. Isto é, no produto de elementos desse grupo, a ordem dos fatores altera o resultado. O pessoal diz que um grupo com essa característica não é comutativo. Um grupo comutativo é dito Abeliano, nome dado em homenagem a Niels Abel, matemático norueguês que precedeu Galois no estudo dos grupos. Por coincidência, Abel teve uma vida tão aperreada quanto Galois e também morreu jovem, com 27 anos.
Galois foi praticamente o primeiro a usar a noção de grupos para estudar a solubilidade das equações. Todo aluno de secundário sabe achar as raízes que dão a solução de uma equação de segundo grau. Existem fórmulas mais complicadas para solucionar equações de terceiro e quarto grau. Mas, ninguém conhece um processo para solucionar equações de grau cinco ou maior. Abel mostrou, em 1824, que uma equação de quinto grau não tem solução. Nessa demonstração, ele já usou as permutações entre as raízes mas não avançou muito no uso dos grupos. Isso foi feito, mais tarde, por Galois que usou os grupos para mostrar que equações de grau igual ou maior que 5 são insolúveis.
O uso intensivo da teoria de grupos em Física teve início quando a Mecânica Quântica estava em seus primórdios, na 
década de 20 do século passado. Consta que o grande físico Eugene Wigner estava enrolado na tentativa de usar as ferramentas da nova teoria quântica no estudo dos átomos e moléculas. Conversando sobre essas dificuldades com seu colega matemático John von Neumann, este lhe perguntou:”você já ouviu falar do Lema de Schur?” Esse obscuro Lema faz parte da teoria de grupos e, até então, só tinha interesse para os matemáticos mais abstratos. Wigner, a partir daí, passou a aplicar intensamente os resultados da desconhecida (pelos outros físicos) teoria de grupos no estudo das ligações entre átomos e moléculas e obteve tanto sucesso que terminou ganhando o prêmio Nobel de Física em 1963. Hoje, a teoria de grupos faz parte da ferramentaria dos físicos teóricos e experimentais de todas as áreas, desde os que pesquisam novos materiais até quem se dedica aos problemas de altas energias.
