A Refração da Luz
Miragens, fibras ópticas, diamantes. Tudo isso se relaciona com a refração da luz.
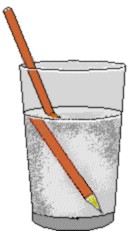
Um feixe de luz se desvia ao passar do ar para a água ou vice versa. Para observar esse efeito basta mergulhar um lápis em um copo com água. Esse desvio se deve a uma mudança na velocidade da luz ao passar de um meio transparente para outro e chama-se REFRAÇÃO DA LUZ.
Nessa seção vamos explicar como ocorre a refração da luz e descrever algumas consequências curiosas e outras muito úteis desse efeito.
O que é a refração da luz.
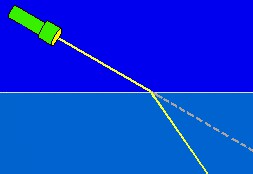
Por que a luz se desvia ao passar de um meio transparente para outro?
Desde o século 19 já se sabia que a luz é uma forma de onda que se propaga com alta velocidade. Mas, essa velocidade depende do meio por onde a luz está se propagando. No ar, a velocidade da luz é quase 300.000 quilômetros por segundo. No interior de um vidro transparente ela se reduz a uns “meros” 200.000 km/s. É essa mudança de velocidade que faz o feixe de luz se desviar ao passar do ar para o vidro.
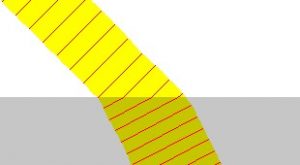
O astrônomo John Herschell explicou esse desvio com uma analogia engenhosa. Ele comparou a onda de luz a uma formação de soldados que passa de um chão rijo (asfalto) para outro mais frouxo (areia). É claro que na areia a velocidade das fileiras de soldados fica reduzida. O resultado disso é duplo: a distância entre as fileiras fica menor e a direção da marcha é desviada. Analogamente, ao passar do ar para o vidro, por exemplo, onde sua velocidade se reduz, a onda de luz se desvia e a distância entre as cristas ( o chamado “comprimento de onda”) fica menor.

A figura ao lado esquematiza esse desvio da luz ao passar do ar para o vidro. A reta imaginária, perpendicular à superfície de separação entre os dois meios, chama-se “normal”.
Há uma relação simples entre o ângulo A que o feixe faz com a normal no ar, e o ângulo B, que faz com a normal no vidro. Na verdade, essa relação relacional os SENOS desses dois ângulos. Ela é:
sen A / sen B = velocidade da luz no ar / velocidade da luz no vidro.
Usando os valores vistos na figura, achamos
sen A / sen B = 1,5.
Esse número (1,5) vai aparecer na próxima seção e será batizado de “índice de refração”. A relação acima é chamada de LEI de SNELL.
O grande matemático Pierre de Fermat concebeu uma explicação para essa relação. Digamos que uma onde de luz vá do ponto A (no ar) até o ponto B (no vidro). Qual será a trajetória seguida pela luz? Existe, é claro, uma infinidade de caminhos possíveis. Três deles são mostrados nessa figura. Será que a luz vai pelo caminho (1), que é uma linha reta sem desvios? Esse, é claro, é o caminho mais curto entre A e B. Ou será que vai pelo caminho (2) no qual passa mais tempo no ar, onde sua velocidade é maior?
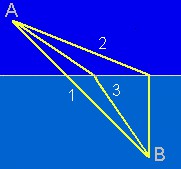
Resposta: o caminho é aquele que segue a Lei de Snell, vista acima. Na figura, é a trajetória (3). Fazendo as contas, verifica-se que esse caminho é aquele no qual a luz gasta o menor tempo para ir de A até B. Qualquer outra opção seria mais demorada. Essa é a essência da explicação de Fermat. E vale em qualquer situação, isto é, a luz sempre percorre uma trajetória de tempo mínimo (não de distância mais curta).
Vale a pena voltar ao caso da marcha dos soldados (veja de novo a figura, se quiser). Se os soldados quisessem forçar a marcha sem desviar ao passar do asfalto para a areia, iriam, na verdade, se atrasar. O caminho que faz um desvio que depende da relação entre as velocidades nos dois pisos (Lei de Snell), não é o mais curto mas é o que economiza mais tempo.
O índice de refração e o desvio da luz.
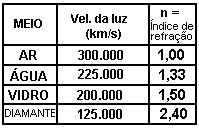
Como vimos na seção anterior, a relação entre as velocidades da luz nos dois meios é chamada de índice de refração. Veja, na tabela ao lado, o valor da velocidade da luz em vários meios. Na última coluna vemos o índice de refração supondo que a luz vai do ar para o outro meio. Então, se a luz vai do ar para o vidro, o índice de refração n é dado pela divisão da velocidade da luz no ar (300.000 km/s) pela velocidade da luz no vidro (200.000 km/s). Logo, n = 1,5.
Quanto maior o índice de refração de um material, em relação ao ar, maior será o desvio da luz quando passa do ar para esse material. Veja, na figura abaixo, o desvio da luz quando passa do ar para os três meios relacionados na tabela acima. Em todos os casos, a luz incide na interface que separa os meios com um ângulo de 60°, para podermos comparar. O desvio é maior para o diamante, que tem o maior índice de refração.
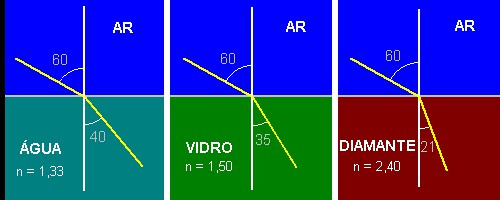
Observe, também, que o caminho da luz é reversível. Isto é, a figura acima mostra a luz passando do ar para o outro meio, mas, também serve para mostrar a luz passando do outro meio para o ar. Por exemplo, se a luz vem da água com um ângulo de 40°, ela passará para o ar com um ângulo de 60°. Portanto, quando o feixe de luz passa de um meio para outro onde sua velocidade é maior, ele se afasta da normal. Essa observação é essencial para entender algumas consequências interessantes que vêm a seguir.
A reflexão total e o ângulo crítico.
Vimos, na seção anterior, que um feixe de luz que sai da água para o ar se afasta da normal. Na figura ao lado, o feixe (AO) vem da água com um ângulo de 40° com a normal. Ao passar para o ar, se desvia e passa a fazer um ângulo de 60o com a normal (OB). Se o ângulo na água for aumentando, o ângulo no ar também aumenta. Quando o ângulo na água chega a 49,75° (CO), o ângulo do feixe no ar passa a ser 90° (OD), isto é, o raio de luz sai rasante à superfície da água. Esse ângulo de 49,75° é o ângulo crítico para a luz que sai da água para o ar. E, se a incidência se der com um ângulo maior que o ângulo crítico, 60° (EO), por exemplo? Nesse caso, toda a luz se reflete na superfície e volta para a água (OF). Isso se chama de reflexão total.
Observe que, quando o ângulo é menor que o ângulo crítico, a luz se reflete e se transmite, ao mesmo tempo. Mas, quando o ângulo é maior que o ângulo crítico, toda a luz se reflete. É por isso que esse fenômeno se chama de reflexão total.
Quanto maior o índice de refração do meio de onde sai a luz, menor o ângulo crítico. Portanto, maior a chance de haver reflexão total. Procure entender bem esse ponto pois logo mais ele será útil.
Explicando as miragens.
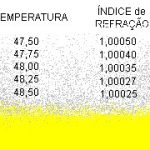
Temperatura em graus centígrados.
Com o que aprendemos nas seções anteriores fica fácil entender como se formam as miragens. Pense no deserto em pleno meio dia. A areia recebe uma enorme energia da luz do sol e se aquece, aquecendo, ao mesmo tempo, as camadas de ar que estão em contato com ela. O ar aquecido fica menos denso e, como consequência, fica com um índice de refração ligeiramente menor que o ar em camadas mais altas e menos quentes. Forma-se o que se chama um “gradiente de temperatura”. Isso é apenas um termo para dizer que a temperatura do ar decresce com a altura a partir da areia. Com isso, o índice de refração aumenta um pouco com a altura. A figura ao lado dá um exemplo desses valores da temperatura e do índice de refração.

Olhe a figura desse beduino. Um feixe de luz que sai das folhas da palmeira na direção da areia passará por camadas de ar com índices de refração cada vez menores. Portanto, o feixe vai gradualmente se desviando até atingir um ângulo tão grande com a vertical que passa a se refletir e começa a subir. Nessa direção de subida, a luz que saiu do alto da palmeira chega aos olhos do beduino. Portanto, ele verá as folhas da palmeira na direção do solo, como se fossem refletidas por um espelho de água. Pelo menos, é assim que o cérebro do beduino interpreta o que vê.
Entenda que isso não é uma ilusão de ótica. O que o beduino vê, realmente, é a luz vindo da palmeira. Apenas a direção (de baixo para cima) é fora do usual e é interpretada erroneamente como devida à reflexão em uma superfície de água. A água é ilusória, mas a palmeira e sua imagem são reais.

Não é necessário ir ao deserto para ver miragens. Viajando de carro em um dia quente é comum a gente se deparar com miragens. O que pensamos ser um espelho d’água lá adiante é apenas uma reflexão do céu e das nuvens que estão no horizonte. Basta substituir o beduino pelo motorista do carro. A água aparente (e ilusória) situa-se a uma distância de uns 300 metros, ou mais, do motorista. Só nessas distâncias é possível haver um desvio da luz passando de descendente a ascendente. Quando o carro se aproxima a água misteriosamente desaparece, ao mesmo tempo que outra surge um pouco adiante.
Agora, resta esclarecer duas coisas que costumam enganar até alguns entendidos. A primeira se refere ao que dissemos acima sobre a temperatura decrescente com a altura. Alguém pode perguntar: “Não é verdade que o ar quente sobe? Então, como é possível que o ar fique mais quente na parte de baixo?” Certo, mas, o que acontece aqui é um “equilíbrio dinâmico”. O ar quente realmente sobe e é trocado continuamente por ar menos quente vindo de cima. Mas, essa troca não é instantânea e forma-se, perto da areia, uma camada rarefeita de ar quente. Juntando os dois efeitos (o aquecimento pela areia e a subida do ar quente) forma-se uma situação que mantém sempre um gradiente de temperatura como foi descrito acima.
A segunda observação leva a uma pergunta: é possível demonstrar que a luz que vemos na miragem provém mesmo de uma refração? Isto é, como poderá o beduino saber se o que está vendo é uma miragem e não um reflexo da palmeira em um lago real, sem se aproximar para tirar a dúvida? A resposta a essa pergunta está na nossa seção EIS A QUESTÃO.
Como um peixe vê uma gata.

A figura ao lado mostra como um peixe vê o corpo de uma garota de biquini que está dentro dágua até a cintura. O peixe está situado a uma respeitosa distância de uns 10 metros da moça e vê essa curiosa imagem. Para entender porque ele vê a moça desse jeito, observe a figura abaixo.
A figura mostra alguns raios de luz que vão do corpo da garota até os olhos do peixe. As trajetórias (1) e (2) vão diretamente através da água até o peixe. Desse modo, ele vê a parte inferior do corpo da moça normalmente. Já um raio de luz (3) que sai dos pés da garota pode chegar aos olhos do peixe depois de uma reflexão total na superfície interna da água. O peixe verá a parte submersa da moça refletida como se houvesse um espelho na superfície. Daí a imagem com as pernas invertidas. Os raios de luz que saem da parte do corpo da moça que está fora da água só podem chegar aos olhos do peixe por refração. O raio (4), por exemplo, que sai quase rasante à superfície, chega aos olhos do peixe na direção (5). O alto da cabeça da moça (Y) será visto na posição (Z). Como o ângulo ZPY é menor que o ângulo YPX, a imagem que o peixe vê da parte de fora do corpo da garota é achatada.
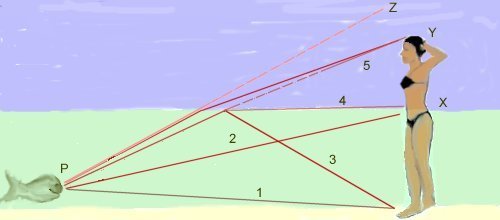
Vale a pena traçar alguns raios extras nessa figura para entender melhor como se forma essa interessante imagem.
Por que um diamante brilha tanto?

Está lembrado do ângulo crítico? Quanto maior o índice de refração de um material transparente, menor o ângulo crítico. Depois que um feixe de luz entra em um material de grande índice de refração, só sai se incidir, internamente, com um ângulo menor que o ângulo crítico.
O diamante tem um índice de refração n = 2,40. Com esse valor do índice de refração, o ângulo crítico do diamante (em relação ao ar) é pouco maior que 24°. Uma vez dentro do diamante, a luz só sai se incidir na superfície interna com um ângulo menor que esse. De 24° até 90° a luz se reflete de volta.
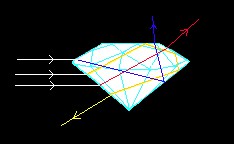
Veja, na figura ao lado, como três raios de luz que entram paralelos entre si acabam saindo em direções completamente diversas. Além disso, como a luz refratada se separa em suas componentes, pode acontecer que entre branca e saia de qualquer cor. A figura está um pouco exagerada nesse aspecto, apenas para ilustrar o efeito.
A lapidação, isto é, a forma como a pedra é cortada, com muitas faces em ângulos variados, ajuda a intensificar esse efeito. Mas, se for um mero vidro, com seu modesto índice de refração 1,50, não há lapidação que consiga reproduzir o brilho de um diamante. Hoje em dia, com luz artificial inundando o ambiente, o brilho de um diamante não é tão impressionante como era à luz dos candelabros dos tempos românticos. Uma pena.
As fibras ópticas e seus usos em comunicação.
Nos últimos anos surgiu uma tecnologia que está revolucionando as comunicações. São as fibras ópticas, que utilizam exatamente o fenômeno da refração que descrevemos.
Uma fibra óptica é um fio muito fino e flexível, feito com um material extremamente transparente. O diâmetro usual de uma fibra óptica é de 50 mícrons, isto é, 0,05 milímetros. O material da fibra é, em geral, a sílica (óxido de silício, SiO2), pura ou misturada com outros materiais controlados. A sílica das fibras feitas atualmente tem um grau tão elevado de pureza e transparência que a luz passa por ela perdendo muito pouca intensidade. Vamos fazer uma comparação da transparência de uma fibra óptica com a transparência de um vidro comum de janela, mesmo um vidro de ótima qualidade. Um vidro de janela tem, normalmente, uns 5 milímetros de espessura. Pois bem, uma janela hipotética, feita com a sílica usada nas fibras, teria de ter uns 10 quilômetros de espessura para absorver o mesmo que a janela de vidro comum de 5 milímetros!
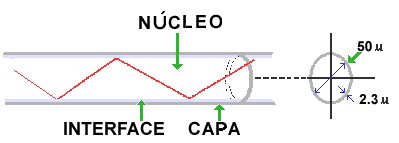
Como mostra a figura, a fibra tem um núcleo de sílica e uma interface de sílica misturada com outro material de menor índice de refração. O conjunto é protegido por uma capa plástica. Por causa da diferença de índice de refração entre o núcleo e a interface, um feixe de luz fica confinado no interior da fibra e viaja por ela como a água em um cano. O ângulo com que o feixe incide sobre a interface é sempre maior que o ângulo crítico, fazendo com qua a luz se reflita totalmente e fique presa no interior do núcleo.
As fibras ópticas são muito usadas, hoje em dia, na medicina e nas telecomunicações, para transporte de voz e dados. Uma fibra é incomparavelmente mais eficiente para transporte de sinais de comunicação que um fio de cobre. Diferentemente de um fio de cobre, a fibra não sofre interferências de campos elétricos e magnéticos. Além disso, usando freqüências ligeiramente diferentes, é possível transmitir milhares de sinais por uma única fibra, sem perigo de aparecer linha cruzada. Hoje em dia, todo o planeta está se transformando em uma enorme teia de fibras ópticas transportando as más notícias do que ocorre no mundo.
Algumas experiências simples sobre refração e reflexão total.
Em nossa seção SUGESTÕES PARA FEIRAS DE CIÊNCIA, temos algumas experiências simples mas divertidas, que ilustram a refração e a reflexão total. Dê uma olhada.
CONDUTORES DE LUZ.
Uma “fibra óptica” feita de água!
REFLEXÃO TOTAL NO AQUÁRIO.
Usando um apontador de laser.
Procure arranjar uma fibra óptica para suas experiências. Hoje a gente encontra até em lojas de presentes, usadas como decoração. Você pode também pedir umas amostras no serviço telefônico de sua cidade. Com a atual privatização desses serviços, não garantimos que você seja bem atendido, mas, não custa tentar.

