A Tensão Superficial
Quem sustenta uma bolha de sabão?
Eis um conceito muito usado mas pouco entendido. Costuma-se ouvir dizer que, devido à tensão superficial, a superfície da água forma uma espécie de pele elástica, como a borracha de um balão de aniversário. Dizer apenas isso não explica muita coisa. Nas seções que se seguem abordamos o tema da tensão superficial de várias maneiras.
Para saber sobre a tensão superficial sem apelar para a matemática.
As moléculas de um líquido interagem entre si de várias maneiras. Uma delas é a atração ou repulsão elétrica, se estiverem carregadas ou se suas cargas positivas e negativas não estiverem igualmente distribuídas no espaço. Além disso, sofrem a ação da gravidade e da agitação térmica. No cômputo geral, se o líquido estiver em um recipiente, como um copo, por exemplo, as forças de atração preponderam e impedem que as moléculas se espalhem pelo espaço.
O líquido ocupa um volume determinado, formando uma superfície bem definida entre ele e o ar circundante. Surge daí uma diferença clara entre as moléculas da superfície e as que ficam internas no líquido. As que ficam dentro interagem com as demais em todas as direções. Em média, portanto, essas interações (ou forças) se anulam mutuamente. Já as que ficam na superfície só podem interagir com as que estão do lado de dentro. Do lado de fora só existe o ar e as moléculas do ar estão tão separadas uma das outras que seu efeito imediato sobre a superfície líquida pode ser desprezado.
O resultado é que a película que fica na superfície sofre uma atração para dentro do próprio líquido. Essa tendência é contrabalançada pela resistência das moléculas de dentro que só podem ceder espaço até certo ponto. Quando o equilíbrio é alcançado a tendência das moléculas superficiais de penetrarem no líquido é equilibrada pela resistência das demais que estão no interior.
Se o líquido for a água dentro de um copo, forma-se uma superfície mais ou menos plana e ligeiramente encurvada para cima nas paredes internas do copo. Se o recipiente for um tubo estreito, a superfície da água assume uma forma côncava, o menisco, como se diz. E se a água estiver em queda livre? Ou, o que é a mesma coisa, se estiver solta dentro de um ônibus espacial em órbita?
Nesse caso, as moléculas da superfície se arranjam de modo a formar a menor área possível para o volume que ocupam. Pode ser demonstrado que essa configuração corresponde à situação de menor energia. Os sistemas físicos gostam de se acomodar em situações de energia mínima. Acontece que, para um dado volume, a forma espacial que tem a menor área é a esfera. As moléculas de água em queda livre se ajuntam de modo a formar gotas esféricas. Isso também explica porque as bolhas dentro de um líquido são esféricas.
Esse fenômeno é descrito como sendo devido à tensão superficial. Observe que a tensão superficial não é nenhuma força ou interação nova, com o mesmo status do peso ou da força elétrica. É apenas um tipo de equilíbrio entre essas forças que já existem no líquido moldando a forma da superfície desse líquido.
Qual a razão desse termo tensão superficial? É fácil admitir que a película de couro de um tambor está tensa. Se fizermos um furo no couro do tambor com uma agulha ele se rasga todo por causa da tensão. Coisa semelhante ocorre na superfície do líquido. Nela se forma uma espécie de pele que é uma camada estreita e tensa, embora a tensão não seja tão grande quanto no tambor. A intensidade dessa tensão depende de que líquido estamos tratando, se ele é puro e da temperatura em que está. Alguns aditivos modificam fortemente a tensão superficial de um líquido. O exemplo mais comum é o dos detergentes que diminuem muito a tensão superficial da água em que são dissolvidos. Com isso, diminui a tendência de formar gotas fazendo com que as moléculas da água tenham maior contato com as fibras dos tecidos. Dessa forma, a sujeira do tecido é mais facilmente deslocada pela água e dissolvida em forma de emulsão.
A tensão superficial de uma gota esférica (com um pouco de matemática).
Imagine uma gota esférica de água com raio R. A pressão do líquido dentro da gota (p1) é maior que a pressão fora dela (p2). Se não, a gota se ajustaria em um menor volume. Digamos que a diferença entre essas pressões seja p = p1 – p2. Esse excesso de pressão deve ser compensado de algum modo para que a gota não estoure. A compensação é fornecida pela tensão superficial na parede da gota. Como vimos antes, as moléculas da superfície da gota são atraídas para dentro, forçando, por causa dessa atração, as moléculas internas. Sendo essa tensão superficial T uma força por unidade de comprimento podemos calcular a força total sobre uma circunferência máxima da gota multiplicando T pelo comprimento dessa circunferência. Obtemos
F1 = 2π R x T.
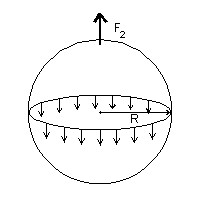
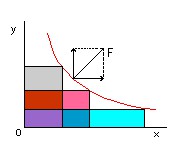
No desenho, F1 é a resultante dos pequenos vetores distribuídos ao longo da circunferência. O excesso de pressão p, multiplicado pela área de um dos hemisférios separados pela circunferência considerada, corresponde a uma força tendendo a separar os hemisférios. No equilíbrio, a componente F2 dessa força, perpendicular ao plano da circunferência que divide a gota, deve ser equilibrada pela força F1 , devida à tensão superficial.
Quanto vale a componente F2?
Se você sabe cálculo integral é fácil achar F2. Se não sabe terá de se contentar com a informação de que F2 = p π R².
Portanto, fazendo F1 = F2, obtemos p = 2 T / R.
Essa é a chamada fórmula de Laplace.
Você pode aceitar esse resultado como um ato de fé mas pode observar que F2 é o produto da pressão pela projeção do hemisfério sobre o plano equatorial, cuja área é a área do círculo encerrado pela circunferência máxima.
Pela fórmula acima vemos que, quanto maior for a tensão superficial T de um líquido, maior a tendência desse líquido de formar grandes gotas (isto é, maior o raio R da gota).
Como se mede a tensão superficial.
Existem vários métodos para se medir a tensão superficial. Vamos descrever um deles em duas variações possíveis de serem realizadas em qualquer laboratório de Física do segundo grau.
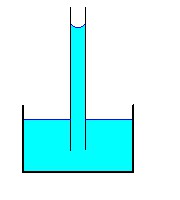
Usamos o chamado efeito de capilaridade. Um tubo muito fino é chamado de tubo capilar por ser, possivelmente, tão fino quanto um fio de cabelo. Introduzindo um tubo capilar em um recipiente com água ela sobe pelas paredes do tubo até uma certa altura. Quem sustenta o peso da coluna de água no capilar é a tensão superficial. No caso, essa tensão se deve à interação entre as moléculas de água e a parede interna do capilar. Ao longo da circunferência de contato entre a água e a parede surgem forças atrativas que levantam a água até que são impedidas pelo peso da coluna. A resultante vertical dessa força é dada pelo produto da tensão superficial (em dinas/cm) pelo comprimento da circunferência interna do tubo (cm). O resultado é uma força que deve ser igual ao peso da coluna de água que subiu pelo tubo. Esse peso pode ser calculado medindo-se a altura da coluna desde o nível da água no recipiente até o menisco, que é a superfície abaulada no alto do tubo. O peso será o produto do volume da coluna pela densidade da água. Igualando-o a T πR² obtemos a tensão superficial T.
A tensão superficial da água é cerca de 0,075 N/m. A do álcool é 0,024 N/m. É mais difícil formar gotas de álcool que de água, nas mesmas condições.
Outro modo de medir a Tensão Superficial.
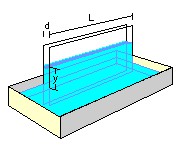A maneira descrita anteriormente é a mais usual para se medir a tensão superficial. No entanto, nem sempre a gente dispõe de um tubo capilar de diâmetro interno bem calibrado. A técnica descrita a seguir é mais simples, mais vistosa e requer apenas duas placas planas de vidro. Use duas placas bem limpas, de 10 x 20 cm, por exemplo. Veja a figura ao lado.
Submergindo as duas placas paralelas bem próximas uma da outra, a água deve subir entre elas por causa da tensão superficial. A pequena distância d entre as placas pode ser mantida usando-se tiras de plástico como separadores.
A força devida à tensão superficial nas paredes internas entre as duas placas é F = 2 T L. Essa força compensa o peso da coluna que é P = m g = ρ ( L y d ) g, onde é a densidade da água.
Igualando F e o peso P obtemos a tensão superficial T = ρ g d y / 2.
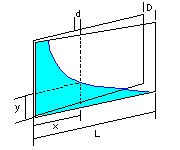
Uma variação legal consiste em colocar as placas formando uma cunha, com o separador só de um lado. A água forma uma superfície curva cuja projeção vertical é uma hipérbole.
Você já deve saber que a equação da hipérbole é y = C / x, onde C é uma constante.
Pela figura vemos que d = D x / L.
Logo, substituindo d na expressão acima da tensão superficial, obtemos:
T = ρ g y D x / 2L . Portanto:
y = ( 2 T L / ρ g D ) / x = C / x .
A curva é realmente uma hipérbole.
Colando papel milimetrado em uma das placas facilita a medida de x e y . Depois de tirar as placas o papel molhado mostra a hipérbole.
Verifique a seguinte propriedade da hipérbole: a área de qualquer retângulo entre ela e os eixos coordenados é uma constante.
UMA QUESTÃO : A força F devida à tensão superficial é perpendicular à linha da água. A componente vertical de F é equilibrada pelo peso da coluna de água. Quem equilibra a componente horizontal?
Nota: Adaptado de um artigo de I. I. Voroyov, na excelente revista Quantum de Janeiro de 1998, pg. 30.
Qual é a espessura de uma bolha de sabão?
Quando queremos dar a idéia de uma coisa fina dizemos: ‘fina como um cabelo’.
Mas, a parede de uma bolha de sabão é milhares de vezes mais fina que um cabelo.
Observe a linha abaixo.
____________________________________________________
Pois bem, a parede de uma bolha de sabão é cerca de 40.000 vezes mais estreita que essa linha!
Em uma escala onde essa linha representasse a espessura de uma bolha de sabão, um fio de cabelo teria um diâmetro maior que 2 metros!
Em números: a parede de uma bolha de sabão tem espessura aproximada de 5 milimícrons, isto é, 5 x 10-9 metros, ou ainda, 0,000000005 metros ou 0,000005 milímetros.
Uma experiência curiosa com a tensão superficial.
Arranje uma taça de vidro bem limpa e encha-a de água até a borda, sem deixar derramar.
Com muito cuidado e mão firme você pode introduzir uma agulha na água (pela ponta fina) e deixá-la cair até o fundo da taça. Quantas agulhas você é capaz de colocar na taça, dessa forma, sem que a água derrame?
Faça a experiência.
Se for realmente cuidadoso poderá colocar mais de 1000 agulhas!
Agora olhe a superfície da água. Você verá que ela está bem convexa, formando uma barriga considerável.
Uma agulha típica tem volume da ordem de 5 mm³. Se a taça tiver 5 centímetros de raio, a área da superfície da água será inicialmente cerca de 7850 mm². Se a altura da barriga chegar a 1 mm, o volume da barriga será cerca de 7850 mm³. Portanto, caberão, em princípio, 7850 / 5 = 1570 agulhas.
Quem impede a água de se derramar pelas bordas enquanto você introduz as agulhas é a tensão superficial. Não faz mal nenhum você pensar na superfície da água, redonda que nem uma barriga de grávida, como se fosse uma espécie de pele elástica que se estica sem se romper, à medida que o volume total (água+agulhas) vai aumentando.
