O Efeito Doppler
Uma cantora correndo a maratona desafina?
Esse efeito, explicado pelo austríaco Christian Doppler em 1843, tem aplicações importantes. Foi por meio dele que aprendemos que o Universo vem se expandindo desde que surgiu no big bang. Mais domesticamente, os meteorologistas usam o efeito Doppler para acompanhar os movimentos atmosféricos e fazer previsões de clima e os policiais do trânsito para multar os apressados.
Para dar uma ideia do que é esse efeito descreveremos uma experiência semelhante à que foi realizada originalmente pelo próprio Doppler.
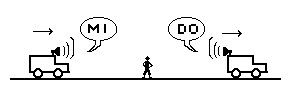
Suponha que um carro está parado a uns 200 metros de você e o motorista toca a buzina continuamente. Digamos que o som da buzina tem uma tonalidade única, correspondente à nota RE, com frequência f = 288 ciclos por segundo. Esta é uma simplificação, é claro, pois as buzinas normais são mais agudas e quase nunca são de uma nota só. Nesse nosso caso, portanto, você ouve um som constante (e irritante) com a tonalidade de RE.
Mas, que acontece se o carro não estiver parado e se aproximar de você com uma velocidade v de uns 120 km/h? Você ouvirá a buzina com uma tonalidade mais aguda, correspondente à nota MI, que tem uma frequência f ‘ de 320 ciclos por segundo.
Se o carro estiver se afastando de você com a mesma velocidade, você ouvirá um som mais grave, correspondente à nota DO, que tem frequência f ‘ igual a 256 ciclos/segundo.
Um resultado semelhante seria obtido se a fonte do som estivesse parada e você estivesse se aproximando ou se afastando dela com boa velocidade.
DOPPLER
Clique no link acima para ouvir o som de uma fonte que se aproxima e depois se afasta de um observador. A frequência do som quando a fonte está parada é de 1000 ciclos por segundo. No início, quando a fonte está se aproximando, a frequência é maior que 1000 c/s. Ao passar pelo observador ela volta a ser de 1000 c/s mas, logo a seguir, ao se afastar do observador a frequência cai para um valor menor que 1000 ciclos por segundo.
Explicação (quase) sem matemática
Eis aqui uma historinha que ajuda a entender a origem do efeito Doppler.
Suponha que todo dia sai um ônibus de Belém com destino a Porto Alegre. Na mesma hora, todo dia, também sai um ônibus de Porto Alegre para Belém. Digamos que a viagem entre as duas cidades dure 10 dias. Você é passageiro de um dos ônibus que saem de Belém. Perguntamos: durante os 10 dias de viagem, com quantos ônibus vindo de Porto Alegre você cruzará?
Com 10, dirá um apressadinho. Errado. Você cruzará com os 10 ônibus que já estão viajando e com mais 10 que sairão de Porto Alegre durante os 10 dias de sua viagem.
Isto é, nos 10 dias de sua viagem você cruzará com 20 ônibus vindo de Porto Alegre.
Digamos que você se interesse pelas notícias de Porto Alegre e cada ônibus que sai de lá traga o jornal do dia (o DIÁRIO de Porto Alegre). Como você cruza com 2 ônibus em cada dia, você poderá ler 2 diários por dia! Quer dizer, a frequência com que você lê os jornais é 2 vezes maior que a frequência com que eles foram produzidos em Porto Alegre.
Agora compare esse surpreendente resultado com o que foi dito acima sobre o tom das buzinas e veja como eles são semelhantes. A frequência percebida por um ouvinte que se aproxima da fonte sonora é MAIOR que a frequência percebida se o ouvinte estivesse parado.
A proporção em que essas frequências diferem depende da velocidade relativa entre a fonte sonora e o ouvinte. Para saber quanto vale essa proporção, só apelando para a matemática. Você entendeu a origem do efeito Doppler. Se quiser saber mais detalhes veja as próximas seções.
Explicação com um pouco de matemática
O efeito Doppler se aplica a qualquer tipo de onda, mas, vamos tratar especificamente de ondas de som.
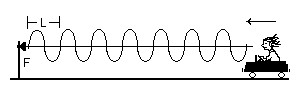
A fonte sonora F emite um som com frequência f que se propaga com velocidade v. Essa velocidade do som no ar é de 330 metros por segundo. Se o som tiver a tonalidade de um RE MÉDIO (sem trocadilho), a freqüência será f = 288 ciclos por segundo. Essa será também a freqüência ouvida por um observador que esteja parado em relação à fonte sonora. Esse observador receberá, em cada segundo, 288 ciclos de onda, cada um de comprimento L. Portanto, a onda se desloca de uma distância f x L, em cada segundo. Ora, esse deslocamento da onda, em cada segundo, é, por definição, a velocidade da onda. Isto é: v = f x L
Mas, digamos que o observador se aproxima da fonte de som com uma velocidade vo. Nesse caso, além dos f ciclos que ele recebia por segundo quando estava parado, receberá mais alguns ciclos extra devido ao seu movimento de aproximação. Com sua velocidade ele se aproxima de vo metros da fonte, em cada segundo. Nesses vo metros estão contidos vo/L ciclos. Logo, a frequência que ele recebe (isto é, o número de ciclos por segundo que atingem seu ouvido) será f MAIS vo/L.
Chamando essa frequência recebida de f ‘ temos:
f ‘ = f + vo/L.
Mas, como vimos que v = f x L, temos L = v/f. Logo:
f ‘ = f + vo.f / L = f ( 1 + vo/v).
Por exemplo, se a nota emitida for um RE com f = 288 ciclos por segundo e a velocidade do ouvinte for de 33 metros por segundo, a frequência ouvida será de:
f ‘ = 288 (1 + 33/330) = 316,8 ciclos por segundo.
Essa frequência é próxima da nota MI (que tem frequência de 320 ciclos por segundo). Quer dizer, o som ouvido não será um RE mas um MI um pouco desafinado.
Se, em vez de se aproximar, o ouvinte se afastar com velocidade vo, a fórmula que obtivemos acima deve ser modificada, trocando o sinal de vo. Isto é, se o ouvinte se afasta:
f ‘ = f ( 1 – vo/v ) .
Usando os números dados acima você pode verificar que a frequência ouvida por um observador que se afasta com velocidade de 33 metros por segundo (que é equivalente a uns 120 km/h) será de cerca de 260 ciclos por segundo. Isso corresponde, aproximadamente, ao som de uma nota DO.
Um engano de Christian Doppler
O austríaco Christian Doppler foi o primeiro a explicar o efeito que tem seu nome e também o primeiro a aplicá-lo erradamente. Ele previu que um som tem sua tonalidade aumentada se a fonte sonora se aproxima do ouvinte. Esse efeito foi verificado experimentalmente pelo holandês Buys-Ballot, dois anos depois da publicação do artigo de Doppler.
Mas, Doppler cometeu um engano em seu artigo que tinha como título Sobre a Luz Colorida das Estrelas Duplas. Pelo título você já pode ver que Doppler pensava que a cor das estrelas era devida ao deslocamento delas em relação ao observador. Por exemplo, uma estrela que se afastasse de nós deveria ser avermelhada pois a luz emitida por ela seria deslocada para menores frequências (lado vermelho do espectro visível).
Na verdade, isto não se dá por dois motivos. Primeiro, o espectro da luz de uma estrela, isto é, a faixa de frequências da luz que ela emite, se estende muito além da faixa visível. Logo, mesmo que esse espectro fosse deslocado, a luz ultravioleta emitida pela estrela seria deslocada para a faixa visível, ocupando o lugar da faixa azul que se deslocou na direção de menores frequências. No fim, a luz visível emitida continuaria tendo componentes de todas as cores e seria ainda branca.
Além disso, para haver um deslocamento apreciável no espectro a velocidade relativa da estrela deveria ser muito grande, próxima da velocidade da luz. As estrelas a que Doppler se referiu em seu artigo não possuem, nem perto, velocidades tão grandes.
Assim mesmo, Doppler estava correto em supor que há um deslocamento do espectro. Hoje se sabe que galáxias distantes estão se afastando com tremendas velocidades e, por causa do efeito Doppler, o espectro da luz que elas enviam e chega até nós é deslocado para frequências mais baixas. É o que se chama deslocamento para o vermelho. Quem primeiro observou isso foi o astrofísico americano Edwin Hubble em 1929. Surgiu dai a idéia de que o universo está se expandindo. Mas, essa já é outra história que comentamos na próxima seção.
O efeito Doppler e a expansão do universo.

Edwin Hubble dentro de seu telescópio
O astrofísico americano Edwin Hubble, em 1929, descobriu que as galáxias distantes estão, quase sem exceção, se afastando muito rapidamente de nós. O espectro da luz dessas galáxias chega até nossos telescópios e espectrômetros apresentando um desvio para o vermelho. Hubble explicou esse interessante fenômeno utilizando o efeito Doppler. Se a velocidade com que a galáxia se afasta for realmente grande, a luz que ela envia e chega até nós terá um desvio para frequências mais baixas, do mesmo modo que o som de uma buzina se afastando fica mais grave.
Na verdade, embora algumas pessoas não concordem, não há nada de especialmente repulsivo na Terra para que as galáxias fujam de nós. O que há, segundo Hubble e a grande maioria dos cosmologistas atuais, é que o Universo está se expandindo.
Essa expansão implica em que, em algum tempo distante, o Universo devia ser muito menor do que é agora, praticamente um ponto, com uma densidade próxima de infinita. Por alguma razão, nesse tempo, ocorreu uma gigantesca explosão, o Big Bang, e a partir daí o Universo vem se expandindo cada vez mais.
Essa teoria do Big Bang tem inúmeras implicações cosmológicas. Até alguns anos atrás, era considerada por muitos como mera especulação. Hoje, porém, já são conhecidas várias comprovações experimentais que concordam com ela. Uma das mais festejadas foi a descoberta, em 1965, por Arno Penzias e Robert Wilson, da chamada radiação de fundo, que ocupa todo o espaço e é exatamente o que os modelos e os cálculos dos cosmologistas previam como decorrente do Big Bang.
Hubble foi homenageado quando teve seu nome usado para o telescópio espacial que hoje está em órbita. As observações desse telescópio confirmam a hipótese do Universo em expansão.
O velho Doppler estava correto, afinal de contas.

