A BRAQUISTÓCRONA
EXPERIMENTO INTERATIVO
A BRAQUISTÓCRONA – CURVA DE MENOR TEMPO
Você quer construir uma rampa entre dois pontos, um mais alto e outro mais baixo, e quer que uma bolinha escorregue por esta rampa no menor tempo possível. Qual é a forma da rampa para conseguir esse objetivo?
Esse foi o problema apresentado pelo físico e matemático suiço Jean Bernouilli no ano de 1696. O próprio Bernouilli já tinha achado uma solução, mas queria saber dos colegas se haveria outra prova diferente.
Vários cientistas da época atenderam o convite e enviaram suas ideias para Bernouilli. Entre eles, Leibniz, o irmão Jacques Bernouilli e Isaac Newton. Todos concluíam que a curva de menor tempo é uma CICLOIDE.
Esse problema ficou conhecido como a busca pela BRAQUISTÓCRONA, palavra vinda do grego e composta por “brakhisto” = “menor” e “chronos” = “tempo”.
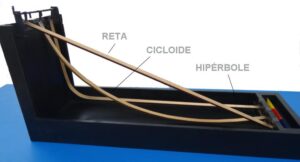
O experimento que vamos descrever ilustra essa propriedade da braquistócrona, a curva de menor tempo. Nele, temos três rampas. Uma delas tem a forma de uma RETA entre os pontos mais alto e mais baixo. Como sabemos, este é o caminho mais curto entre os dois pontos. A segunda tem a forma de uma cicloide. E a terceira tem a forma de uma hipérbole, escolhida por ter uma queda quase vertical no início da rampa.
Antes de realizar o experimento, vale a pena discutir o possível resultado e dar palpites sobre qual rampa será a mais rápida.
No alto das rampas existe um mecanismo simples para apoiar as bolinhas e soltá-las todas ao mesmo tempo acionando uma alavanca.
Coloque as bolinhas em seus lugares no alto, mas, antes de acionar a alavanca prepare o dispositivo que fica no final das rampas.
Esse dispositivo é simplesmente uma cantoneira de alumínio que vira quando atingida por uma bolinha. Posicione a cantoneira de modo a ser virada pela primeira bolinha que chegar ao final. Desse modo, a bolinha mais rápida ficará isolada de um lado da cantoneira e as outras ficam do outro lado.
As bolinhas liberadas caem muito rapidamente e é bem difícil vê-las durante a queda. Essa é a razão de usarmos a cantoneira para separar a bolinha ganhadora.
Fazendo o experimento, você verifica que a bolinha mais rápida é justamente a que cai pela rampa na forma de cicloide.
DISCUSSÃO TEÓRICA:
É claro que este experimento não prova que a cicloide é a braquistócrona. Apenas mostra que ela ganha da reta e da hipérbole.
Para provar isso, precisamos de matemática. E foi isso que os cientistas que atenderam o desafio de Bernouilli fizeram.
Os métodos usados pelos contemporâneos de Bernouilli usavam truques de cálculo e geometria disponíveis na época. Posteriormente, vários matemáticos utilizaram uma técnica matemática chamada de “cálculo das variações”. Trata-se de um procedimento que permite achar uma função (no caso, a forma da rampa) que torna máximo ou mínimo o valor de uma variável (no caso, o tempo de queda). Essa técnica foi desenvolvida por grandes matemáticos como Euler e Lagrange.
Jean Bernouilli usou um processo bem engenhoso para achar a braquistócrona. Esse processo aproveitava resultados de ótica (refração) e técnicas desenvolvidas por Pierre Fermat.
A demonstração de Bernouilli está descrita detalhadamente em uma das referências que damos abaixo [1] e não precisa ser reproduzida aqui.
A CICLOIDE:
A cicloide, além de ser a braquistócrona, tem outras propriedades interessantes que podem ser exploradas em uma aula.
Essa curva pode ser obtida pelo deslocamento de um ponto da periferia de um círculo rolando, sem deslizar, por um plano horizontal.
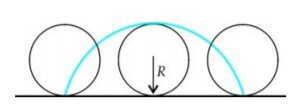
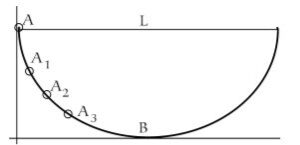
E mais: a ciclóide também é uma isócrona. Em uma pista de skate na forma de uma cicloide, uma partícula leva o mesmo tempo para completar uma oscilação, independente do ponto de onde for solta. Huygens usou essa propriedade em seus relógios.
Para traçar uma cicloide ou uma hipérbole você pode usar as tabelas contidas no link abaixo:
http://www.seara.ufc.br/sugestoes/fisica/mec3.htm
SUGESTÕES PARA A SALA DE AULA:
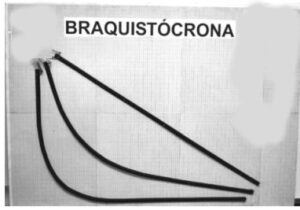
O professor pode reproduzir esse experimento em sala de aula sem muita dificuldade. É fácil montar as três rampas em uma única prancha de madeira usando tiras de borracha ou plástico e bilas de vidro ou bolinhas coloridas achadas em casas de bijuterias. Com esse equipamento simples, é possível ilustrar as propriedades descritas acima da cicloide.
REFERÊNCIAS:
[1] Graciliano Batista, Cleuton Freire e José E. Moreira, Física na Escola, Vol. 7, pg.58 (2006).
Disponível em: http://www1.fisica.org.br/fne/phocadownload/Vol07-Num2/v13a101.pdf
[2] M. Desaix, D. Anderson e M. Lisak, European Journal of Physics, Vol. 26, pg. 857 (2005).

