Caixa de Fósforos e Chaves
Objetivo
Uma demonstração surpreendente da aceleração rotacional e do atrito exponencial de um cabo enrolado.
Descrição
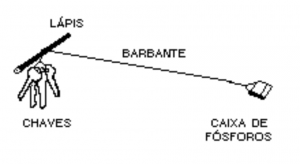Use um barbante de 1 metro ou mais de comprimento e amarre, em uma ponta, um molho de chaves e, na outra ponta, uma caixa de fósforos de papel. Estenda o barbante passando sobre um lápis que serve de polia. Com uma mão você segura a caixa de fósforos e, com a outra, segura o lápis. As chaves ficam penduradas bem perto do lápis e os fósforos um pouco abaixo do nível do lápis, com o barbante esticado quase horizontalmente.
Quando você soltar a caixa de fósforos, o que acontece? Será que o molho de chaves atinge o solo?
Análise
Tente a experiência pois o resultado é surpreendente: as chaves não atingem o solo. Duas propriedades físicas, pelo menos, estão envolvidas nesse resultado. Quando o barbante vai encurtando a velocidade rotacional da ponta com os fósforos aumenta rapidamente, como uma bailarina que gira e fecha os braços, diminuindo o momento de inércia I. Para conservar o momento angular L = I w, a velocidade angular w aumenta. O barbante gira em torno do lápis e se enrola nele várias vezes. Entra em ação o segundo efeito: o atrito entre o barbante e o lápis cresce exponencialmente com o número de voltas.
Esse efeito explica porque é fácil prender um objeto pesado, como um barco, por exemplo, apenas amarrando-o com uma corda em um mastro.
O matemático Leonard Euler (pronuncia-se “Óiler”) achou uma fórmula para esse efeito: F = f ekx, onde F é a força do lado pesado e f é a força necessária para equilibrar F. k é o coeficiente de atrito entre o mastro e a corda e e = 2,728… é a base dos logaritmos naturais. x é o ângulo de enrolamento, cada volta correspondendo a 2
.
Por exemplo, se o coeficiente de atrito for 1/3 e a corda der 3 voltas, qual é a força necessária para segurar um puxão de 5 toneladas?
O ângulo x é: x = 3×2 = 6. Logo, k x = 2
Usando a fórmula de Euler, obtemos:
Se o atrito for um pouco maior e o número de voltas for 5 ou mais, não é nem necessário segurar a outra ponta pois a força f fica minúscula.
Material usado
Um molho de chaves.
Uma caixa de fósforos de papel.
Um lápis.
Um pedaço de barbante de 1 metro ou mais.
Dicas
A experiência é simples mas o resultado é surpreendente e a física é sofisticada. Elabore um pouco mais o estudo do atrito exponencial e explore o uso do princípio da conservação do momento angular.
