Solução Questão 1 – Fluidos
1) Paradoxo hidrostático
Solução:
A força FA é igual à força FB.
Esse é o chamado Paradoxo Hidrostático. A força que o líquido faz sobre o fundo do recipiente só depende da área da base e da altura da coluna de líquido.
Na explicação abaixo, vamos chamar a densidade da água de ρ e π = 3,14159…

No cilindro (A) a pressão na base é ρ.g.H e a área da base é π.R², logo, a força sobre a base é FA = ρ.g.H.π.R². Mas, π.R².H é o VOLUME do cilindro (A). Logo, FA é exatamente o peso da água contida em (A). Agora imagine uma parede cônica (inexistente, por enquanto) na forma do recipiente (B), que divide a água de (A) em duas parte, uma interna (I) e outra externa (E). Na parede do cone imaginário a força total de (E) sobre (I) deve ser igual à força total de (I) sobre (E), já que o líquido está em equilíbrio. A componente vertical da força de (E) sobre (I) deve ser igual ao peso de (E).
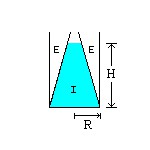
Agora, vamos colocar uma parede cônica real (fina e rígida) separando (I) de (E). As forças continuam as mesmas, é claro, pois continua a haver equilíbrio. Então, retiramos a água de (E). Como a parede cônica é rigida, isso não muda nada. Um micróbrio nadando em (I) não tomaria conhecimento que a água foi removida de (E). Isto é, a parede cônica rígida deve exercer a mesma força vertical para baixo que o peso de (E), mesmo quando o líquido de (E) é retirado!
Voltamos, finalmente, ao recipiente cônico (B). A força hidrostática sobre a base de (B) é o peso da água em (I) MAIS a força vertical para baixo exercida pela parede cônica lateral que, como acabamos de ver, é exatamente o peso de (E). Portanto, a força hidrostática sobre a base de (B) é a soma dos pesos de (I) e (E), que é igual ao peso da água em (A), que, por sua vez, é igual à força que age sobre a base de (A).
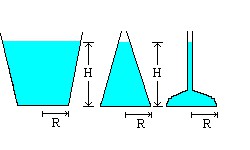
Podemos extrapolar: todos os recipientes mostrados na figura ao lado, que têm a mesma base e água até a mesma altura, sofrem a mesma força sobre suas bases.

