Solução Questão 2 – Eletricidade e Magnetismo
2) Um circuito interessante
Solução:
A resistência entre A e B é de 5/6 de Ohm.
O circuito do problema equivale a um circuito em forma de cubo. Compare as figuras.
Os pontos A e B são diametralmente opostos. Por simetria, podemos ver que os nós 1, 2 e 3 devem ter o mesmo potencial, pois cada um está separado por uma resistência de 1 Ohm do mesmo ponto A. Logo, podem ser agrupados em um só ponto que chamaremos de ponto 123.
O mesmo acontece com os nós 4, 5 e 6, que serão agrupados como um ponto único 456.
Temos então dois grupos de resistências em paralelo (123) e (456).
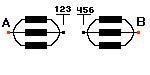Cada uma das seis resistências restantes está ligada entre um dos pontos 1, 2 ou 3 com um dos pontos 4, 5 ou 6.
Logo, essas resistências estão em paralelo entre si, formando um conjunto que se conecta em série com os outros dois.
Agora é fácil concluir o problema.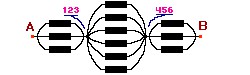
A resistência entre A e B será de 1/3 + 1/6 + 1/3 = 5/6 de Ohm.
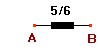
Esse tipo de problema fica facilitado pela seguinte observação. Desenhando o cubo de lado 1 em coordenadas retangulares, observamos que as coordenadas de todos os vértices são 0 ou 1. Vamos definir a ORDEM de um vértice (ou nó) como sendo a SOMA de suas coordenadas. O ponto B, por exemplo, tem ordem 1 + 1 + 1 = 3. O ponto A tem ordem 0.
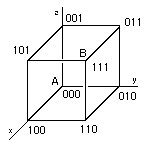
Aplicando uma diferença de potencial entre A e B observamos, por simetria, que os vértices que têm a mesma ordem têm o mesmo potencial. Logo, podem ser agrupados em um único nó, como fizemos na solução do problema.
Se você pensar um pouco verá que esse truque vale não só para um cubo mas para qualquer poliedro regular com resistências iguais em cada aresta. Tente achar uma fórmula geral para a resistência equivalente entre os dois pontos opostos de um poliedro regular (cubo, octaedro, dodecaedro e icosaedro). Não é muito difícil.
DESAFIO
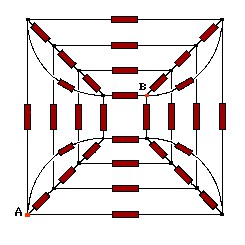
Calcule a resistência entre os pontos A e B do circuito ao lado. Cada resistência vale 1 Ohm. Observe que só há ligação nos pontos indicados com um nó.
Esse último circuito pode ser identificado como um arranjo espacial na forma de um cubo tetra-dimensional, ou hipercubo. Cada nó pode ser localizado por um conjunto de 4 coordenadas retangulares. A e B são pontos diametralmente opostos do hipercubo.
SUPER DESAFIO
Resolvendo os problemas acima você achou a resistência entre pontos diametralmente opostos de um cubo (3 dimensões) e de um hipercubo (4 dimensões). Agora mande brasa e calcule a resistência entre dois pontos diametralmente opostos de um hipercubo de n dimensões, para um n qualquer. Cada aresta desse hipercubo tem uma resistência de 1 Ohm.
